Draw Length Vs. Release Velocity
Table
Of Contents
Background .:. Top
The bow has been around for nigh on 5 millennia. It was developed in Africa, as an alternative to spears and spread up into the European and Asian continents (Shen/Sze). Since its development, the bow had become one of the most useful tools in existence, before the advent of the musket. It made hunting easier and more people could do it, not just the able bodied ones who needed to hurl spears at their quarry. Bows also gave range advantages, and depending on the bow, that range could be over 300 yards (Sims). Bows come in a variety of forms, the most common being longbows, recurves, and compounds. Longbows, also known as stick bows, are just one straight or slightly curved piece of material, usually wood, though recently fiberglass or a mix of the two has been used. The longbow was the preferred bow of most of the Europe subcontinent, especially the English (Sims), and while it has impressive range, power, and reload time, it also is one of the more physically taxing types of bows. This is due to the need to be able to hold the force of the bow while drawing it, which is more commonly known as draw weight. Recurves help ease this problem, as their shape has a curve away from the shooter at each end, which add to the “cast”, or throwing power of the bow, while reducing the strength needed to pull the string back (Williams). Of course, the compound bow, the most recently developed, uses the mechanical advantage of pulleys to allow for bows to have incredible power, while allowing the shooter to be able to hold the draw easily (Williams). Drawing them, however, forces the shooter to pull the string back to about mid draw with the entire power of the bow against them, and only after breaking the mid draw point does the advantage kick in. Yet all bows share their basic properties. The limbs are what store energy and their resistance to movement is what gives them their power (Allain). The more resistant, the more power. This increases the draw weight of the bow. Another factor that adds to draw weight is draw length.
Draw length is the distance between the string at full draw, and the back of the bow (Schuh). As the bow is drawn, the force required to pull it increases. The principle is the same as a spring, the more compressed it is, the more force is required to compress it. The bow’s limbs act as springs, storing potential energy during the draw, which is converted into kinetic energy as they snap back into their original shape, and send the arrow flying (Schuh). As such, both the total draw weight, and the draw length of a bow affect the power it has to send an arrow. The arrows themselves determine how far they travel, if shot from the same bow. A light arrow will travel farther, but will not absorb as much of the energy as a heavier one, and thus may not be an accurate representation of the bows capabilities. Also, different arrows have different spine, or flex (Williams). Due the the “archer’s paradox” (Shen/Sze), the arrow actually bends during flight, as the string has to push it around the bow. The different spine of the arrows contributes to different flight patterns, and may not absorb as much of the bow’s energy. However, most modern arrows are made to specifications that keep their spine consistent from arrow to arrow. Thus it is fair to say that the draw length has direct ties to the force applied to the arrow, and consequently, the arrow’s velocity as it is released.
Statement of the Problem .:. Top
The purpose of this experiment is to find out the correlation, if any exists, between draw length and arrow release velocity.
Hypothesis .:. Top
I believe that the results will be a linear correlation between draw length and arrow velocity, with shorter draw lengths yielding slower arrows and longer ones producing quicker arrows, meaning that the kinetic energy of ½ mv2, where m is the mass of the arrow, and v its velocity, will equal the potential energy of ½ kx2, where k is the spring constant of the bow, and x is the distance drawn. Draw length is defined as the distance from original string position to the point to which it is pulled to, and arrow velocity as the speed the arrow has upon release.
Method .:. Top
To test the hypothesis, a device used to measure the arrow’s velocity at varying draw lengths was needed. The one used had the bow and the measurement apparatus affixed to the same board, with the arrow being tied with fish line to the measurement apparatus. The apparatus itself consisted of a NTE 3102 Opto Interrupter, which was a light sensor, two discs of lightweight cardboard, and a foam wheel. The cardboard discs were cut into circles, with one being larger than the other. These discs were then glued to the foam wheel so that it was centered perfectly on both. A hole was then punched in the rim of the larger disc, which would become the outside disc once assembled. Next, a larger hole was drilled through the discs and foam, through which a bolt would be placed. The hole was widened to accommodate two small ball bearings, which would allow the wheel to turn freely on its bolt. The bolt was then affixed to a short board, with some washers acting as a spacer between the board and the inner, smaller, disc. Next the light sensor circuit was made, giving it wires for power and for the oscilloscope to sense it, and was attached to the main board with the wheel, so that the outer disc, with the hole in it, ran smoothly between the sensor’s groove. This would allow the oscilloscope to see whenever the hole passed the sensor, giving the time between each pass. The last piece was a block of wood that was made to move back at set intervals and hold the bowstring until it was released. This was accomplished by gluing two dowel stubs into holes on the underside of the block, which would then insert into evenly spaced holes on the main board. On the top of the block, another hole was drilled and a third dowel stub was used as a pull pin for holding the bowstring. A string was then tied to the arrow that went back and wound around the wheel, thus causing the wheel to spin as the arrow was fired, and the oscilloscope would measure the time between each rotation.
The rotations are a
set distance, 22 inches in this experiment, thus the velocity the arrow
achieved was able to be found using the equation of distance divided by time.
Due to the arrow’s deceleration over time, only the first two rotations were
measured. The measurements were taken using a LeCroy
9314 AM oscilloscope, making the time measurements accurate down to 1*10-4
units, and had 10 megabytes of RAM, giving it the processing capability to read
the pulses as the sensor fired. The data received was in milliseconds as the
arrow would spin the wheel multiple times per second. Thus, the equation that
was used in this experiment was (43 ¾ )/(T*10-3),
which yielded results in the units of inches per second. The total distance the
arrow travelled during its recorded time was 44 in., but ¼ was the distance
lost on the first rotation as the wheel was zeroed with the hole positioned
just in front of the sensor, thus making the first rotation ¼ of an inch
shorter. Three trials of each draw length were done, and the draw length
increased by four inch intervals. Once the measurements were taken, the SA
units were converted to metric for less complicated values.
|
|
|||
|
|
|||
|
|
|||


Data .:. Text .:. Excel .:. Top
Results
.:. Top
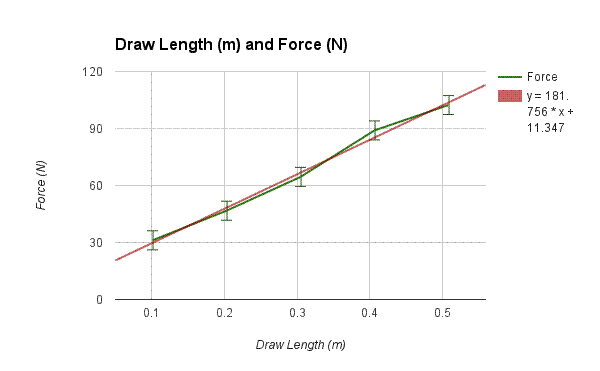
This graph shows the increase in force due to the increase in draw length using the formula F=k*d, where F is force, k is the spring constant, and d is the draw length.. It mirrors the effect of the arrow’s velocity in that it is mostly linear. This too can be attributed to the constant k value, which makes the force of the bow increase linearly with the draw length. This graph should have the slope equal to the k value, thus it is 181.756 Nm. The force increased as the draw length increased due to a larger amount of potential energy stored in the bow. This energy increased as the draw length increased, showing the linear correlation. This graph also has an uncertainty of 63.973, as found by analyzing the graph.
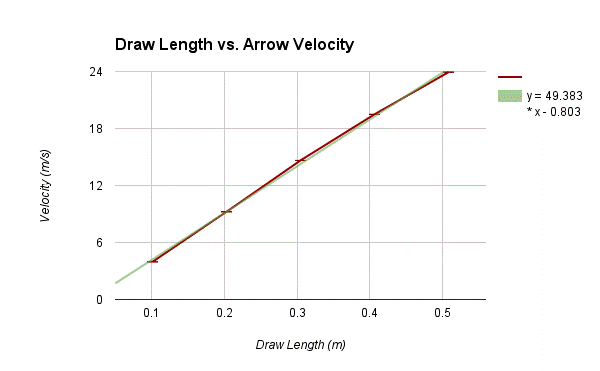
This graph displays the velocity as a function of draw length using the formula v=√(k/m) * d, where v is the velocity, k is the spring constant, m is the mass of the system, and d is the draw length. The result is linear, as was predicted, due to the k value being constant. The red line is the data, and the blue trendline displays the most likely equation. The slope of this equation should be equal to √(k/m), where k is the spring constant and m is the total mass of the system. Due to the error margin being so small, an uncertainty was unable to be obtained from this graph.
Conclusions .:. Top
The data shows a linear correlation between the draw length of the bow and the release velocity of the arrow. This supports the hypothesis that it would be linear, and that there exists a spring constant for a bow, which scales the velocity linearly in proportion to the draw length. This is due the mass being kept constant and the potential energy stored in the bow being equal to the kinetic energy of the arrow as it is released, thus forcing the k value to be constant as well. The second graph displays this, with its slope being equal to √(k/m), which allows it to become linear. The k value was found, however, using the force data from the second graph. When graphed, the k value is 181.756 Nm, as the trendline for the first graph shows. This however, differs from the calculated k value found using the formula F = kx. Using the raw data, both the force and the distance were known, leaving the k value to be solved for. Though each data point held a different k value, the average was 233.727 Nm. The difference between the two k values is 51.971. The reason the two are different is that the k value from the graph is including the mass of the system in its calculations, which would result in a lower k value than the one calculated from the formula, which does not factor in the mass of the system. The reason it is called the mass of the system, is because it was not just the weight of the arrow that the bow had to cast, rather it was the weight of the arrow plus the mass of the measuring system: the wheel and string.
To improve the research, rather than have the arrow tied to a wheel, a more elaborate chronograph could be used, one that required the arrow to be shot through it, but not have the arrow hindered by extra weight and drag, which caused it to lose some of the force being put into it, and thus slow down. That force was transferred to the wheel, however, making the wheel spin at near the same rate as the arrow was traveling, making the data proportional to the arrow’s velocity and the bow’s power output. Also, the release, though brief, was not as smooth and consistent as it could have been, especially at the increased draw, as the bowstring would have enough pressure to hold the release pin into place, making the pulling of it harder; plus the bowstring had a tendency to rise with the pin, which also contributed to a less consistent release. The bow itself could have been held more securely, ensuring the each trial was a replica of the last, and the draw length could have been found to a more accurate degree by having a machine pull the string back to a preset distance. Also, while originally intended to be in inches per second, converting to metric units made the calculations easier, and thus if the experiment were to be started in metric, then there is less chance of data being skewed through conversion error.
Some areas of error include, but are not limited to, the arrow being slowed down by the added weight of the string and wheel, the zeroing of the wheel’s hole not being exactly ¼ of an inch in front of the sensor each trial, the actual distance the draw was at each interval may not have been quite exact, and the surrounding conditions may have affected the bow’s properties, which would change its performance and spring constant. Also the force was measured with a scale oriented for pounds, then converted to kilograms and finally Newtons.
Bibliography .:. Top
Allain, Rhett. "How Much Energy From a Bow Goes Into Kinetic Energy of the Arrow?" Wired.com. Conde Nast Digital, 8 Dec. 2014. Web. 21 Nov. 2015.
http://www.wired.com/2014/12/much-energy-bow-goes-kinetic-energy-arrow/
Quantum. "Physics Buzz: How'd They Do That Tuesday: Bow and Arrows."Physics Buzz: How'd They Do That Tuesday: Bow and Arrows. Physics Buzz, 24 Feb. 2009. Web. 21 Nov. 2015.
http://physicsbuzz.physicscentral.com/2009/02/howd-they-do-that-tuesday-bow-and.html
Schuh, Dwight R. Bowhunter's Encyclopedia: Practical, Easy-to-find Answers to Your Bowhunting Questions. Harrisburg, PA: Stackpole, 1987. Print.
Shen, Qi, and William Sze. "Arrows." Arrows. N.p., n.d. Web. 21 Nov. 2015.
http://archeryphysics-mrsmith08.awardspace.com/arrow.html
Sims, Lesley, Dominic Groebner, and Jane Chisholm. The Usborne Book of Castles. London: Usborne, 2002. Print.
Schuh, Dwight R. Bowhunter's Encyclopedia: Practical, Easy-to-find Answers to Your Bowhunting Questions. Harrisburg, PA: Stackpole, 1987. Print.
Williams, John C., and Glenn Helgeland. Archery for Beginners.
Chicago: Contemporary, 1985. Print.
Related Links .:. Top
http://www.real-world-physics-problems.com/physics-of-archery.html
Has some info about shooting bow and arrows in general. Similar to above links.
https://arxiv.org/ftp/arxiv/papers/1511/1511.02250.pdf
Basically my IA but more detailed about the specifics of the bow and arrow.
http://www.meta-synthesis.com/archery/archery.html
More stuff on archery and physics.
All about the arrow’s flight and how the bow applies its force.
http://www.offthegridnews.com/survival-hunting/bow-hunting-compound-vs-traditional-bows/
Hunting with bows. I learned stuff about bow hunting, and since I am a hunter, it was cool.

