An Analysis of the Relationship between the Air Pressure and Muzzle Velocity of an Air Cannon
Lyubomir Gankov
Table
of Contents (Go Up)
Introduction
Method
Results
Data Processing and Presentation
Conclusion
Background (to Table of Contents)
In the twenty-first century, the term ‘air cannon’ most commonly refers to a
hobbyist-build pneumatic weapon, which fires small projectiles for the
amusement of its builders. A colloquial term for an air cannon is “spud gun”,
in reference to the popularity of potatoes as a projectile in such devices.
Some variants of the spud gun feature a combustion chamber rather than a
pneumatic mechanism for launch of potatoes (and other projectiles)[1].
While mostly used for entertainment, there are commercial applications of the
air cannon, such as the cleaning of storage silos, bins and hoppers in cement
processing plants. This is exemplified by the AirBoost® Air
Blaster[2], which is used to “clean the jamming or coating in any wall...
and assist in a resistance free flow of the material”. No matter the
application, be it amateur or commercial, the principles underlying the air
cannon remain the same.
The concept of the air
cannon is based upon the principle of conservation of energy, which states that
energy is conserved. In the case of the air cannon, the potential energy of the
pressurized air is converted into kinetic energy upon the firing of the cannon,
with this kinetic energy propelling the projectile out of the cannon. This can
be expressed through the following equations:
Ek =
½(m)(v2)
(1)
Ep =
½(V)(P2)
(2)
Ek = Ep
(3a)
½(m)(v2) =
½(V)(P2) (3b)
Where Ep is potential energy (J), Ek is
kinetic energy (J), m is mass (kg), and P is pressure (Pa)
The work done to compress air into the barrel can be expressed
through the follow equation:
ΔW = PΔV
W = ∫PΔV
W = ½(V)(P2)
Where W is work done (J), P
is pressure (Pa), and V is volume (m3)
Pressure is defined through Boyle’s Law, which correlates pressure
and volume inversely at a constant temperature:
P = (nRT)/(V)
Where P is pressure (Pa), n
is moles of gas (mol), R is the characteristic gas constant (8.31 J mol−1 K−1), T
is temperature (K), and V is volume (m3)
In this case, Boyle’s Law is used to demonstrate that as moles of
gas (air) are added into the tank, which is of a fixed volume, pressure in the
system increases. Thus, the work done in compressing air into the barrel is
exponential, and is stored in the air cannon’s tank, which serves as a
pneumatic capacitor, in that it stores energy based on a differential of
pressure (between the inside and outside of the tank). The work done to
compress the air into the tank is equal to the potential energy of the air inside
the tank due to the law of conservation of energy. The kinetic energy
transferred into the projectile is therefore fired with the energy put into the
system with the work done to compress the gas.
There are several potential variables to be adjusted in the design of an air
cannon, including barrel diameter, barrel length, air tank pressure, air tank
volume, and projectile weight[3].
While of these variables have the potential to affect the projectile velocity,
this study will analyze the effect of air tank pressure on muzzle velocity
exclusively. However, even in this more narrow approach, there is still a broad
range of issues to be addressed. One is the composition of the projectile
itself; the density of the projectile affects the distance it has the potential
to travel based upon the kinetic energy it can absorb[4].
Furthermore, the shape of the projectile affects the airflow through the
barrel, as if it is not uniform (such as in the case of the potato, a popular
projectile), not all of the potential energy that is released will be imparted
as kinetic energy into the projectile as some of the air will escape around the
object[5].
Statement
of Problem (to Table of Contents)
The purpose of this investigation is to determine the effect that air pressure
has on the initial muzzle velocity of a projectile fired from an air cannon.
Hypothesis (to Table of Contents)
The relationship between air
pressure, the independent variable, and resultant muzzle velocity, the
dependent variable, will be a linear positive correlation. This will occur due
to the underlying conservation of energy inherent to the pneumatic system of an
air cannon: as air is compressed, the exponential amount of work required to
pressurize it results in the potential energy in the system, from which
velocity is quadratically derived.
Air pressure is defined as
the gauge pressure of a tank (a closed volume), and muzzle velocity is defined
as the initial velocity of a fired projectile. The control variables include,
but are not limited to, the size and mass of the projectile, ambient air
pressure and temperature, volume of the air tank, and the length and diameter
of the cannon’s barrel.
Experimental
Set-Up (to Table of Contents)
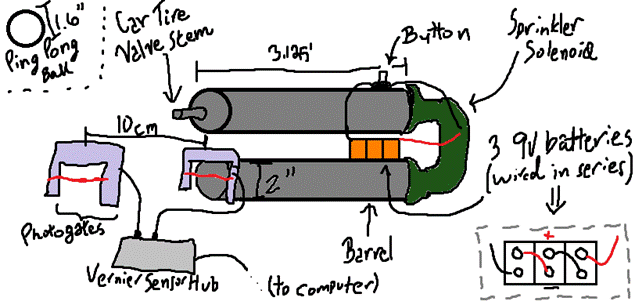
(Diagram not to scale)
The cannon is placed flat on a table, with the photogates in front
of the barrel, in order to minimize external sources of error and isolate the
effects of the relationship between pressure and muzzle velocity.
Materials (to Table of Contents)
- Cannon
a.
(1) 2” (diameter) x 10’ length of PVC pipe (for
tank/ barrel)
b.
(2) 2” to 1” PVC reducers
c.
(1) 1”(diameter) x 6” length of PVC pipe (for
connecting solenoid with reducers)
d.
(1) 1” Anti-Siphon Sprinkler Valve
e.
(1) 2” PVC End Cap
f.
(1) Car Tire Valve Stem
g.
(1) Air Gauge (not pictured above)
h.
PVC Primer and Glue
Cannon Wiring*
.
(3) 9V Batteries
a.
(3) 9V Battery Snap Connectors
b.
(1) Rotary Button
c.
Electrical Tape**
Tools
.
Drill
a.
Drill Bits
b.
Jigsaw (for cutting PVC pipe)
Data Collection
.
(1) ping pong ball
a.
(2) Vernier photogate sensors
b.
(1) Vernier Sensor Hub
c.
(1) Computer
d.
(1) Air compressor
Safety Equipment
.
(1) Ball-catching device***
a.
(1) Pair of Safety glasses
b.
(1) Set of earplugs
* No additional wires were necessary, as the snap
connectors, solenoid, and button all came with adequate lengths of wire.
** A soldering iron could be substituted in order
to establish and maintain connections between wires.
*** In this experiment, a small cardboard box,
stood up to face the cannon, was used to catch the fired projectiles.
Procedure (to Table of Contents)
Set up the working environment and have the air cannon assembled. Prepare the box
for ball-catching, and put on earplugs and safety glasses.
First, fill the air tank
with the desired air pressure, starting at 10 PSI. Then, load the ping pong
into the barrel. Turn on the data collection in Logger Pro, and launch the ball
by toggling the solenoid. Repeat this process for a total of 10 trials at each
given PSI. Upon the completion of 10 trials at a PSI, increase the PSI by an
increment of 10 PSI (up to and including 100 PSI). The end result will be a
10x10 data table of time values for PSIs between 10 and 100.
Data
Processing and Presentation (to Table of Contents)
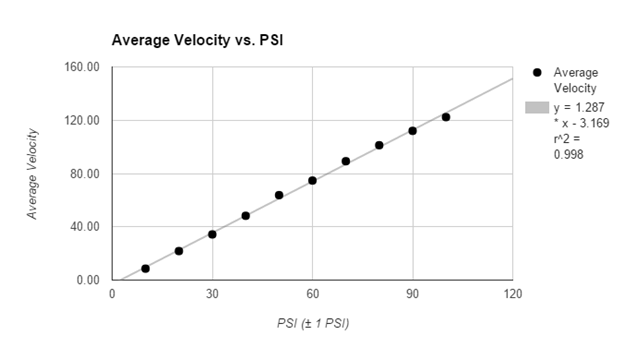
Table 1: Average Velocities at PSI (in increments of 10 PSI)
|
PSI (± 1 PSI) |
Average Velocity (m/s) |
Uncertainty (m/s) |
|
10 |
8.59 |
0.0095 |
|
20 |
21.78 |
0.0167 |
|
30 |
34.28 |
0.0253 |
|
40 |
48.26 |
0.0378 |
|
50 |
63.77 |
0.0501 |
|
60 |
74.70 |
0.0624 |
|
70 |
89.22 |
0.0732 |
|
80.00 |
101.23 |
0.0913 |
|
90.00 |
111.99 |
0.102 |
|
100.00 |
122.30 |
0.117 |
Figure 1: Graph depicting average velocities (m/s) versus tank
pressure (PSI) with line of best fit (generated in Google Spreadsheets)
Evaluation (to Table of Contents)
The hypothesis, which
predicted that the relationship between the air pressure and muzzle velocity of
an air cannon would be a positive linear correlation, was validated by the data
gathered. After a total of 100 trials, with 10 individual trials performed for
each desired PSI (from 10 to 100, in integer increments of 10), the average
muzzle velocities correlated in a positively linear fashion to the air tank
pressure values. The R2 value for the data
set is 0.998 (as calculated through Google Spreadsheets), which shows that the
correlation is almost entirely linear. The justification for the hypothesis,
based on the law of conservation of energy, was that since the energy into the
system should equal the energy out of the system, the velocity and pressure
should be correlated linearly. The following equations show the mathematical
derivation of this principle:
Ek = ½(m)(v2)
(1)
Ep = ½(V)(P2) (2)
Ek = Ep (3a)
½(m)(v2) =
½(V)(P2) (3b)
v =
(P)(V/m)½ (4)
Given that pressure and resultant velocity are correlated linearly
with a constant of volume and mass through the law of conservation of energy, this
experiment could be conducted with other volumes of tank or alternate
projectiles and would yield very similar results.
As the experiment progressed, with trials being conducted at higher pressures,
the uncertainties grow larger. However, for the range of pressures tested (10
PSI to 100 PSI), the uncertainties do not significantly affect the data
gathered, and thus has little bearing on the outcome of the experiment.
Error
And Experimental Improvements (to Table of Contents)
While this lab made use of
accurate sensors for the gathering of time data (for velocities), there are
nonetheless points that potentially merit improvement. One such area is the use
of a more accurate pressure gauge. The gauge used had an uncertainty of ± 1
PSI, which is very large relative to the ± 0.001 m/s of the Vernier photogates.
Instead of using an analogue pressure gauge, a digital one could be used; this
would most likely take the form of a digital tire pressure meter. However, the
inherent risk of such a meter is that in order to measure pressure, some air
leaks out as the meter makes use of the tire stem. The tradeoff between air
released and accuracy in measurement of air pressure can be circumvented
through the use of a built-in digital sensor, though.
Another source of error is
the ratio between the diameter of the ping pong ball and the air cannon barrel.
This ratio is 1.6”:2”, or 0.8. Thus, not all of the air released through the cannon
imparts work onto the ball; a certain percentage of the air is ‘lost’ (about
35%, based on the areas of the ball and barrel, when these are viewed as
circular cross-sections). This came about due to materials available; PVC pipe
is only sold in specific diameters, and these diameters do not coincide with
the diameters of any common small sports balls. One of these two diameters
would have to be changed in order to mitigate the error that results from the
loss of air pressure stemming from the disparity in diameters. The easier of
the two to mitigate would be the diameter of the ball, as there exist many
non-standard balls (not used for official sports), while it would be
significantly more difficult to procure pipe of a nonstandard diameter.
Another instance of error in
this experiment is the shape of the ball, and the manner in which it interacts
with the photogates. Since the ball is spherical, it is very difficult for it
to pass through both photogates with the same point of its surface triggering the
sensor, at least with the influence of gravity and air drag acting upon it.
Thus, the time data gathered is not wholly exact, as it does not reflect the
precise moments in which the ball was within the sensor array.
A potentially significant
source of error is the surrounding air pressure encountered by the ping pong
ball as it is launched from the air cannon. While the photogates were set up
10cm from one another in order to minimize the effect of air pressure, the very
light ping pong ball still is effected by air drag. In order to truly minimize
this, the test could be conducted in a zero-gravity environment; however, since
this is practically infeasible, the test could instead be conducted with
projectiles of higher mass. This is such because the inertia of an object
depends on its mass, and thus the ping pong ball is more affected by the air
resistance than a projectile of higher mass would be (as an object of higher
mass has greater inertia). However, the diameter of the higher-mass object
would have to be around equal (less than or equal to) the diameter of the
barrel in order for the error to be truly mitigated.
A further source of error is
the length of the barrel, as the distance the ball travels before it encounters
the photogates affects its velocity. The barrel is not frictionless, and
therefore the ball is slowed by the friction of the sides of the barrel in
conjunction with the air resistance. The effect of a longer barrel on a ping
pong ball would be detrimental to the experiment, as it would noticeably alter
the data gathered. A shorter barrel would be beneficial in the case of the ping
pong ball, as it would minimize friction between the ball and the barrel and
thus minimize the effect on the velocity of the ball as it goes through the photogates.
However, in the case of a more massive projectile (either in size or in mass),
a shorter barrel may negatively affect the data gathered as the ball may not
have enough time to speed up (since heavier objects have a greater inertia).
Thus, the optimal barrel length is dependent on the diameter and mass of the
projectile selected. For the experiment conducted, a shorter barrel might prove
beneficial so as to attempt to mitigate the effect of barrel friction on the
data gathered. Likewise, the volume of the air tank is a variable that, if
changed, could potentially mitigate error. PSI is a unit that measures the
pressure of a container independent of volume; thus, an increase of volume
could have a meaningful effect on the outcome of the data. The volume of the
air tank would have to be tailored to that of the barrel (as it is recommended
that the volume of the two be equivalent), which is further dependent upon the
projectile used. In the case of this experiment, the volume of the air tank was
roughly equivalent to that of the barrel; thus, an increase or decrease in the
volume of the air tank without a proportional change to the volume of the
barrel could actually end up being a detriment to the experiment.
Another potential (minor)
source of error is the natural fluctuations in ambient temperature and air
pressure: in order to mitigate whatever minute bearing this factor has on the
data gathered, the experiment could be conducted in a temperature and pressure
controlled-environment.
A final source of error is
the condition of the ball used through the experiment. Ping pong balls, being
hollow and made of soft plastic, are prone to external damage. After a certain
number of trials, (of being launched from an air cannon) the ball ceases to be
spherical. Even though the he deformities gathered by the ball over the course
of the experiment are all rather minor, the use of several balls so as to
mitigate any deformities required could alleviate some error inherent in the
design of the experiment. However, with this solution, the masses of the balls
would have to be similar so that a new source of error is not introduced.
Overall, while there are only several major sources of error present due to the
design of the experiment (ratio between ball and pipe diameters, ball mass,
uncertainty introduced by analogue pressure gauge) there are many smaller
sources of error that could be accounted for in order to produce a truly
accurate set of data, that controlled for all but two variable so as to isolate
the relationship between air tank pressure and muzzle velocity.
Bibliography (to Table of Contents)
[1]"US Air Force Measures Potato Cannon Muzzle Velocities."
MIT Technology Review. N.p., 8 May 2013. Web.
29 Nov. 2015. <http://www.technologyreview.com/us-air-force-measures-potato-cannon-muzzle-velocities>
[2]"ABO-Home-page." ABO-Home-page. N.p., n.d. Web. 30 Nov. 2015.
<http://www.airboostiso.com/airblaster.htm>.
[3]Wise, Daniel G., and Mark A. Mitchell. Universal Air Gun Launch
System (1992): n. pag. Defense Technical
Information Center. United States Government. Web. 29 Nov. 2015.
<http://www.dtic.mil/dtic/>
[4]"Theory/physics behind the Spudgun."
The Spudgun Technology Center. N.p., n.d. Web. 29 Nov. 2015.
<https://www.spudtech.com/content.asp?id=6>.
[5]Carl E. Mungan, “Internal Ballistics of
a Pneumatic Potato Cannon”, European Journal of Physics Vol. 30
(2009) 453-457
Related
Links (to Table of Contents)
Not How To
Build An Air Cannon – The very first web page about air cannons, made circa
1993. Details Bill Mills’ air cannon design.
Spudgunner
Air Cannon Designs – Compilation of several practical air cannon designs.
Lu Laboratories Air Cannons
– The air cannon development of Chris Lu, featuring three iterations (Marks I –
III).
Internal
Ballistics of a Pneumatic Potato Cannon – A short research paper detailing
the mathematics of a pneumatic potato cannon.
Pneumatic Cannon
– A series of posts detailing the construction of an air cannon, designed to be
mounted onto a 1/5 scale Sherman tank.
Pneumatic
Antenna Launching Systems – Web page dedicated to pneumatic antenna
launching systems. Very similar to air cannon in construction, has many related
links of its own.