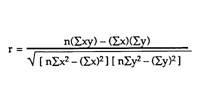Power Output vs. Temperature Equilibrium
By Justin Dowd
Table
of contents:
Heat is the amount of energy a particle has and is associated with the movement of atoms. Energy transfers from one object to another due to collisions with each other (W. Clowes and Sons, Stamford Street and Charing Cross). Energy can be transferred through four different ways such as conduction, convection, evaporation and radiation. In 1701 Sir Isaac Newton anonymously published in a journal called “Philosophical Transactions” his version of the temperature scale using a thermometer using linseed oil and also presented his Law of cooling which states that the rate of heat change is proportional to the difference in temperature of an object and its surroundings (Newton) (Eric Weisstein). Evaporation occurs through heat transfer by phase and radiation transfers energy by photons and can be transmitted through empty space. If one particle has considerably more energy than another the transfer of energy will be greater than objects with similar amounts of energy because of a greater difference in energy. Conduction transfers energy through direct physical contact like a pot on a hot burner. Convection occurs with fluids or gases that create currents due to a difference in temperature like currents in the Earth’s Mantle (Hyperphysics). For example, a hot object will transfer its heat to the surrounding air heating it up. Due to the convection process this air will naturally move away from the hot object and colder air will fill its place, thus creating a mild cooling effect. Because the hot air will not remain in one place the hot object will not be able to retain heat as effectively. Natural forces such as wind also create a amplified forced convection effect by pushing the pockets of air directly away and in turn significantly hindering the object's ability to retain heat (Tufts School of Engineering).
The purpose of this investigation is to determine the temperature equilibrium based on power output (Watts) with its surroundings such as air and the effects convection has on temperature equilibrium.
I believe that as the temperature equilibrium based on the power output will be affected by the rate of convection and also increase exponentially and graphically display an exponential growth graph. The controls of this experiment will be the thermometer, nichrome wire and electrical tape. The independent variable of this experiment will be the power output measured in volts as well as the other object (air or water). The dependent variable will be the temperature equilibrium reached based on power output.
Materials:
1. Variable voltage filtered power supply
2. Thermometer
3. A stand
4. A spool of nichrome wire
5. Electrical tape
6. Wires
7. A fan
8. Amp. Meter
9. Volt Meter
Extension cord (if needed)
Setup:
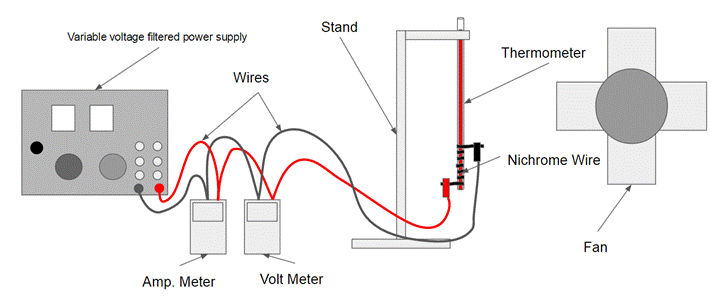
*Note: The electrical tape is not shown in this diagram
1. Get Materials.
2. Get out the spool of nichrome wire and cut a 15cm piece of nichrome wire from the spool.
3. After that get out the thermometer and carefully wrap the nichrome wire around the bulb (Bottom of the thermometer) leaving about 3cm sticking out on both ends.
4. Then cut a strip (About 5cm) of electrical tape and wrap it around the nichrome wire.
5. Now place the thermometer in the clamp and gently secure the thermometer so the bulb is pointing towards the ground.
6. Get out the Variable voltage filtered power supply, the volt meter and the amp. meter and set the amp meter to the 10 DCA setting and the Voltmeter to 20 DCV setting.
7. Now set up the wires in the proper configuration and attach the positive side to one end of the nichrome wire and the negative side to the other end.
8. Now turn the Power supply on and move the voltage dial on the power supply until the voltmeter displays 0.1 volts.
9. Wait until the thermometer appear to have reached a temperature equilibrium and record its voltage, amperage and temperature.
10. Now move the voltage dial on the power supply up by another increment of 0.1 volts and wait for the temperature to reach equilibrium and record its voltage, amperage and temperature.
11. Repeat step 10 about eight more times.
12. After this turn the voltage dial all the way down, turn of the power supply, and wait for the thermometer to reach room temperature.
13. Next, get out the fan, plug it in, position so it facing towards the thermometer, turn it on and repeat steps 8 through 12.
14. Clean up materials.
|
Control |
|||
|
Current (amps) |
Voltage (Volts) |
Power (Watts) *Calculated using P = I * V |
Temperature (Celsius) |
|
0.07 |
0.1 |
0.007 |
20 |
|
0.15 |
0.2 |
0.03 |
21 |
|
0.21 |
0.3 |
0.063 |
23.5 |
|
0.28 |
0.4 |
0.112 |
28 |
|
0.35 |
0.5 |
0.175 |
33 |
|
0.42 |
0.6 |
0.252 |
39 |
|
0.49 |
0.7 |
0.343 |
46 |
|
0.56 |
0.8 |
0.448 |
54 |
|
0.63 |
0.9 |
0.567 |
62 |
|
0.7 |
1 |
0.7 |
70 |
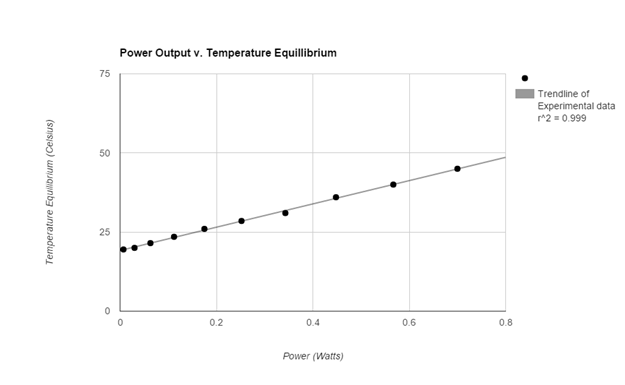
Data (experimental)
|
Experimental (with fan) |
|||
|
Current |
Voltage |
Power (Watts) *Calculated using P = I * V |
Temperature |
|
0.07 |
0.1 |
0.007 |
19.5 |
|
0.15 |
0.2 |
0.03 |
20 |
|
0.21 |
0.3 |
0.063 |
21.5 |
|
0.28 |
0.4 |
0.112 |
23.5 |
|
0.35 |
0.5 |
0.175 |
26 |
|
0.42 |
0.6 |
0.252 |
28.5 |
|
0.49 |
0.7 |
0.343 |
31 |
|
0.56 |
0.8 |
0.448 |
36 |
|
0.63 |
0.9 |
0.567 |
40 |
|
0.7 |
1 |
0.7 |
45 |
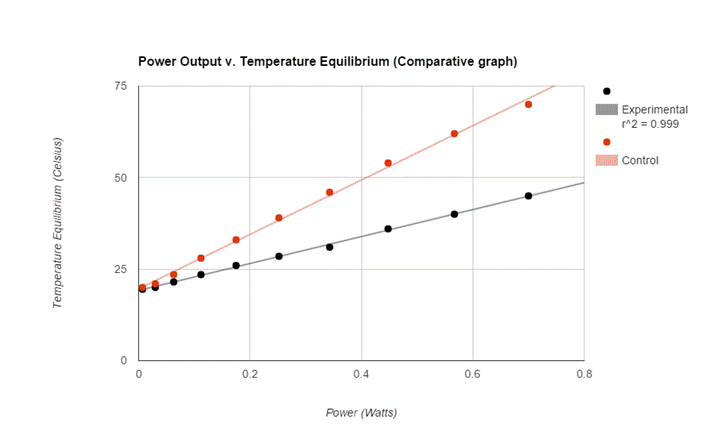
Comparative Data/ Calculations
|
Control |
Experimental |
|
|
Correlation (R coefficient) |
0.998 |
0.999 |
|
Line of best fit |
74.3x + 19.5 |
36.8x +19.2 |
|
Slope (Degrees Celsius / Watt) |
74.3 |
36.8 |
|
Difference of the slopes |
37.5 |
|
Calculations
|
Correlation Coefficient |
Power Formula |
|
Purpose- Determine whether there is a correlation between Power (Watts) and Temperature equilibrium (Celsius) and assess the validity of the results.
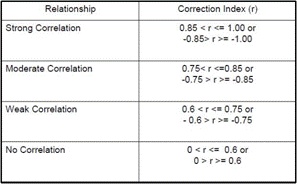
Notes- The answer is a R value which is to be interpreted based on the how far away it is from a perfect correlation which has a R of -1 and 1
Chart for the strength of a correlation
|
Power (Watts) = Current (amps) * Voltage (Volts) Purpose- To determine the Power output in Watts based on the information provided by the Voltmeter and the Amp. Meter to then compare it to the temperature equilibrium. |
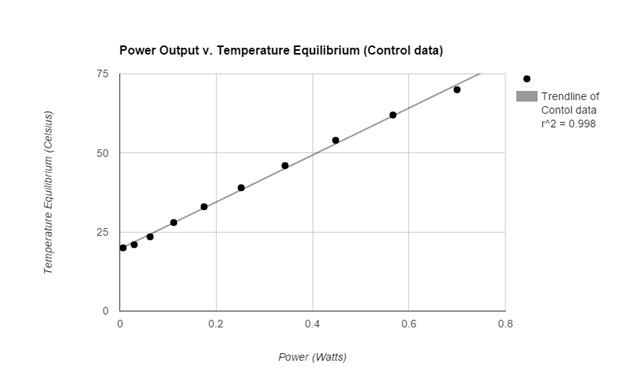
The graphs of both the control and the experimental data both appear analytically to be linear. To further support this mathematically the linear correlation coefficient for the control data having an R value roughly of 0.998 (1 is considered to be perfect correlation) supporting the notion that the graph is linear. More so the experimental data had an R value of 0.999 supporting its linearity. The temperature equilibrium of the Control group changed at a rate of 74.3 degrees celsius per Watt while the experimental group’s temperature equilibrium changed at a rate of about 36.8 degrees celsius per Watt. Therefore the effects of the increased convection (wind) reduced the rate of temperature equilibrium by 37.5 degrees per Watt.
Due to analytical data provided by the graph my hypothesis was wrong in regard to expecting the graph to be exponential nature of the graphs; however my hypothesis was correct in stating that the rate of convection will impact the temperature equilibrium.
There could be errors in this experiment caused the imprecise ability to visually measure the temperature on the thermometer. Also the Volt and Amp. Meter would not consistently remain on the desired voltage and amperage (usually off by plus or minus 0.01) which may have affected the results of the experiment. Moreover, there may be error in the experiment from potentially not waiting long enough for the temperature to reach equilibrium.
To improve the result from the experiment and minimize errors one could use a digital thermometer to get more precise data (avoiding rounding) for the temperature. Also using more precise volt meters and amperage meters may help minimize the uncertainty of the measurement. To also help minimize this problem one could use a Variable voltage filtered power supply with a more sensitive and accurate voltage dial. Lastly, error in the experiment could be minimized by waiting a longer period of time after one believes it has reach temperature equilibrium to make sure it is the exact temperature equilibrium.
Relevant Links:
-http://www.tufts.edu/as/tampl/en43/lecture_notes/ch5.html – This helped learn about convection and how that applies to my study and cooling in general.
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatra.html - This gave me some good background information on heat transfer.
- http://rstl.royalsocietypublishing.org/content/22/260-276/824.full.pdf+html – This is a document that Newton contributed to about heat transfer and cooling.
-http://scienceworld.wolfram.com/physics/NewtonsLawofCooling.html – This gave me the equation for Newton’s law of cooling.
-http://vlab.amrita.edu/?sub=1&brch=194&sim=354&cnt=1 – This is a lab on Newton’s law of cooling
Bibliography
"Convection." EN43ME Lecture Notes. Tufts School of Engineering, n.d. Web. 22 Jan. 2016. <http://www.tufts.edu/as/tampl/en43/lecture_notes/ch5.html>.
"Heat Transfer." Hyper Physics. N.p., n.d. Web. Dec.-Jan. 2015. <http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatra.html>
Newton, Isaac. Philosophical Transactions of the Royal Society of London. Vol. 22. London: Royal Society, 1701. The Royal Society. Web. 5 Dec. 2015. <http://rstl.royalsocietypublishing.org/content/22/260-276/824.full.pdf+html>.
"Newton's Law of Cooling -- from Eric Weisstein's World of Physics."Newton's Law of Cooling -- from Eric Weisstein's World of Physics. WolfRamResearch, n.d. Web. 16 Dec. 2015. <http://scienceworld.wolfram.com/physics/NewtonsLawofCooling.html>.
"The British Almanac." Google Books. W. Clowes and Sons, Stamford Street and Charing Cross, n.d. Web. 22 Jan. 2016.