The air cannon is a novelty that has been used to shoot potatoes, t-shirts, water balloons, and just about anything else that can fit down its barrel. A few more extreme (read: costly) homemade experiments have lead to recognition by science magazines, such as Gary Arold and John Gill's cannon equipped with two 1,000-gallon tanks and 100-foot barrel (Amanda). However, the use of compressed gasses to store power is an important physics concept because of its versatility. The pistons in the engine of your car, for example, use the energy provided from an expanding gas and translate it into rotary motion. In the case of a gas that is rapidly expanding due to deflagration, or burning (Rohrbach). Analyzing its work output can be difficult due to the fact that "combustion is fast and it very rapidly raises the temperature of gas" (Mark). For this reason, it is easier to interpret the data collected from a compressed gas and observe the laws that are correlated with it than it is to do the same with combustion. In this way, we can assume that the temperature of the compressed air is constant, and limit our investigation down to two variables (the independent and dependant variables) because of the Ideal Gas Law.
Energy is stored in an air cannon using the principles of Bernoulli's Equation, which correlates volume and pressure inversely. That is, when volume gets smaller, pressure gets larger. As our volume will be constant (the size of the tank), we need to will manipulate the moles of gas inside the tank to increase air pressure. We can do this because of the correlations stated by the Ideal Gas Law.
The Ideal Gas Law states that, in any (ideal) gas, pressure, volume, moles of gas, and temperature are related:
PV = nRT
...where R=8.3145 J/mol*K is the gas constant. The volume of the gas is also constant, in our case, as the air tank will remain constant. As described above, we will be assuming that temperature is constant. This leaves us with only pressure and moles of gas, the former of which will be controlled by the latter.
As the pressure builds up inside the air tank, upon releasing the valve, the gas within the tank will flow to the area that has lower pressure (Basics of Air Velocity, Pressure and Flow). Upon finding the weak spot (projectile), the gas pushes onto the area with force according to the equation F=PA and accelerates the projectile with the same force following F=ma (Carl).
The purpose of this investigation is to determine the effect that air pressure has on the muzzle velocity of a projectile in an air cannon.
We believe that increasing the air pressure will speed up the projectile's muzzle velocity logarithmically. This theory seems to make sense if you look at it in parallel with hydrostatic pressure; in the first x meters below the surface of a liquid you go, pressure increases greatly, but going another x meters below that does not double the pressure. That is to say, it takes exponentially more work to to continue increasing pressure at a constant rate. In terms of the air cannon, this means that it will, if the parallel stands, take exponentially more work to increase the tank's pressure enough to continue increasing the projectile's velocity at a constant rate; in other words, increasing the air pressure at a constant rate will increase the projectile's velocity logarithmically.
The variables that will be incorporated into this study include air pressure (independent variable) and muzzle velocity (dependant variable). Air pressure is defined to be the gauge pressure inside of a closed volume, in this case the air tank. Muzzle velocity is defined to be the velocity of a projectile as it exits the barrel of the cannon. Constants include, but are not limited to: the size of the tank in which air will be compressed, the diameter and length of the barrel, the size and mass of the projectile, and the ambient temperature and pressure of the environment.
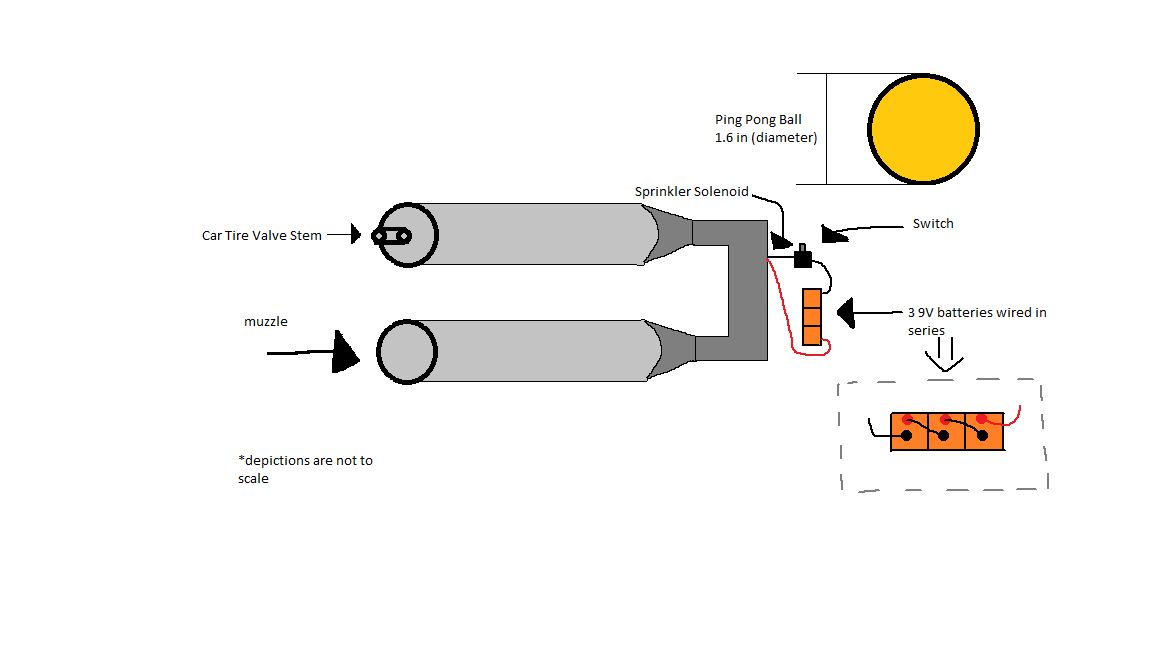
* No additional wires were necessary, as the snap connectors, solenoid, and button all came with adequate lengths of wire.
** A soldering iron could be substituted in order to establish connections between wires.



| PSI (± 1 PSI) | Average Velocity (± 0.001 m/s) |
| 5 | 2.81 |
| 10 | 8.59 |
| 15 | 16.13 |
| 20 | 21.78 |
| 25 | 30.51 |
| 30 | 35.03 |
| 35 | 41.72 |
| 40 | 48.26 |
| 45 | 54.34 |
| 50 | 61.33 |
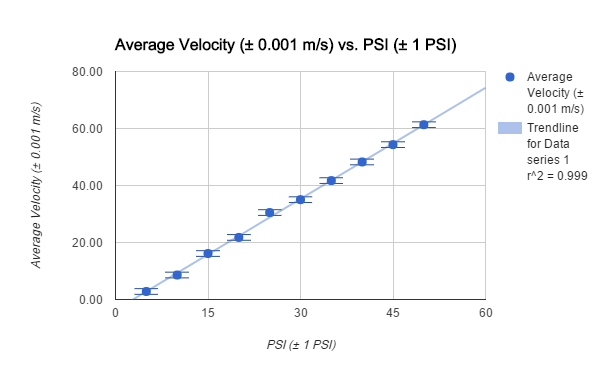
From the data gathered, we can discredit our hypothesis, which predicted a logarithmic relationship between the air pressure and muzzle velocity. Upon analyzing our data's line of best fit (R^2 value of .999 calculated via Google Spreadsheets), we saw that pressure and muzzle velocity correlate in a linear fashion. Initially, we believed that the work done by the compressed air had to increase exponentially to maintain a linear increase in velocity, resulting in a logarithmic correlation. Contrary to our hypothesis, the linear correlation shows that the muzzles work output increased in a constant manner. The linear function y=mx+b gives us y=1.30x-3.68, considering the uncertainty will give us a maximum of y=1.36x-5.36 and a minimum of y=1.25x-2.17. The uncertainty of velocity can almost be neglected when comparing with the uncertainty of pressure.
Instead of the logarithmic correlation that we predicted, the linear correlation between the data points suggests that the output of work through the barrel increases as a constant. This conclusion, however, may be due to the use of a lightweight (2.7g) ping pong ball which does not require much energy to eject from the barrel. We believe that although the our hypothesis did not prove to be true in this experiment, it may still be accurate for projectiles of a higher mass.
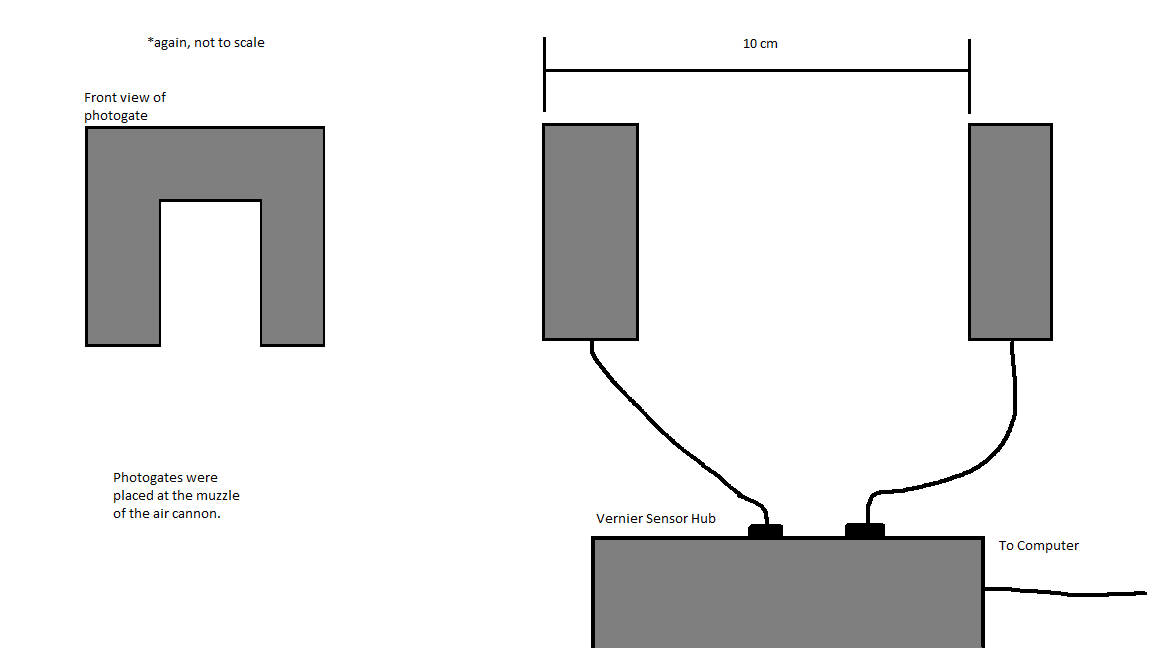
This lab used photogates in an effort to minimize or mitigate any error in data gathering regarding the velocity of the ping pong ball. Despite this, however, the pressure gauge was a potential source of error. The gauge used in our experiment has an uncertainty of ± 1 PSI. This is significant when compared with the 0.001 m/s uncertainty of the Vernier photogate, as it is within our interest to minimize or at least match the decimal places of uncertainty on both devices. Replacing the analog pressure gauge with a digital pressure gauge to increase the precision is an alternative solution.
Due to the poorly planned construction of the cannon and the nature of standard PVC pipe sizes, there are more adapters than were required. These unnecessary adapters create unsmooth areas which change the flow rate, thereby influencing the amount of force exerted onto the projectile as the gas escapes around it. It would be better to make it a near 1:1 ratio in terms of the barrel diameter to that of the ball, however this would require fully customized parts instead of standard PVC pipe. This is a more costly alternative, but also yields more flexibility, such as in the type of projectile. Potentially the most significant limitation of this experiment was the projectile we used, a 1.6 in. diameter ping pong ball with a weight of roughly 2.7 g. This lightweight, spherical object creates significant drag when launched, not to mention the ball has to come out of a 0.4 in. larger barrel. It is not hard to think of how the ball will bounce around within the barrel prior to exiting the muzzle, which makes customization of pipes even more important. Yet, in addition to that, replacing the projectile with a more aerodynamic and/or denser object to reduce drag, or the simplest solution is just perform the experiment and collect the data inside a vacuum chamber, this solution even allow us to accelerate beyond ping pong ball's terminal velocity and get a better picture of how does the velocity of projectile behave when applying higher pressure.
www.popsci.com/gadgets/article/2010-01/air-cannon-sends-pumpkins-3700-feet A large-scale air cannon, for shooting pumpkins.
www.wired.com/2010/11/the-physics-of-punkin-chunkin/ Some basics physics behind pumpkin cannons.
www.iontrap.wabash.edu/publications/AJP_80_24_rohrbach_air_cannon.pdf Reference for the math behind modeling the exit velocity of an air cannon.
www.kiledjian.elac.org/phys%20001/Ballistics%20of%20Air%20Gun.pdf Describes how compressed gasses are used in cannons to launch projectiles.
www.validyne.com/blog/application-note-basics-of-air-velocity-pressure-and-flow More about fluid mechanics, outside of just air cannons.
Carl E. Mungan, "Internal Ballistics of a Pneumatic Potato Cannon", European Journal of Physics Vol. 30 (2009) 453-457
Amanda Schupak, "How It Works: The Artillery-Grade 600 MPH Pumpkin Cannon", Popular Science (2015) <www.popsci.com/gadgets/article/2010-01/air-cannon-sends-pumpkins-3700-feet>
Z. J. Rohrbach, T. R. Buresh, M. J. Madsen, "Modeling the exit velocity of a compressed air cannon", Am. J. Phys. American Journal of Physics (2012) <www.iontrap.wabash.edu/publications/AJP_80_24_rohrbach_air_cannon.pdf>
Mark Denny, "The Internal Ballistics of an Air Gun", The Physics Teacher Vol. 49 (2011) <www.kiledjian.elac.org/phys%20001/Ballistics%20of%20Air%20Gun.pdf>
"Basics of Air Velocity, Pressure and Flow", Validyne Engineering Blog (2013) <www.validyne.com/blog/application-note-basics-of-air-velocity-pressure-and-flow>