The Effect of Dropping a Bouncy Ball from Different Heights on Rebound Percentage

 

Bhargavi Korlipara, Kristen Elder, and Colette Petersen

IB Physics II, 3B

 Return to Research:

 

Table of Contents:

 

1. Introduction

2. Method

3. Results

4. Data Table/Graphs

5. Conclusion

6. Bibliography

 

Introduction:

 

Research Question: What is the effect of dropping a bouncy ball from different heights on its rebound percentage?

 

Statement of Purpose: The purpose of this investigation is to find out the relationship between the height a bouncy ball is dropped from and the height it bounces up to.

 

Background:

            The original bouncy ball or Superball™ was created by Wham-O Manufacturing Company in 1965. They are produced by compressing plastic under about 3500 pounds of pressure per square inch. Some bouncy balls can bounce over three stories high (Superball™ History). Bouncy balls bounce because the rubber they are made of compresses upon hitting the ground. After a brief moment, the ball returns to its original shape, pushing up against the ground and spring into the air. The size of the ball matters because the larger it is, the more it can compress and expand again. The height matters because the higher it is dropped from, the more force there is to compress the ball. When a ball is dropped, it’s velocity increases, and it’s acceleration is 9.81 m/s/s down. As the ball hits the ground, it’s velocity decreases until it reaches 0. When the velocity is 0, it’s compressed as much as possible. The velocity then changes direction and moves up until the acceleration slows it down (Bouncing ball physics).

            In this experiment, a small bouncy ball will be dropped from various heights (10 heights, for 5 trials each); the rebound percentage will be calculated by observing videos of the experiment and seeing how high the ball bounces up for each trial.

 

Hypothesis: If the height from which a bouncy ball is dropped is raised in increments of 20cm, respectively, from 20cm-200cm, then the bouncy ball dropped from 200cm will exhibit a greater rebound percentage.

 

Variables:

Independent Variable: Heights from which the ball is dropped

 

Dependent Variable: Percent rebound of the bouncy ball

 

Controlled Variables: Bouncy ball used, surface bounced off of, technique in which ball was dropped (initial height was measured from base of ball).

 

Method:

 

To set up the experiment, two meter sticks were taped on top of one another, starting from the base of a flat wall. A video camera was then angled based upon the heights from which the bouncy ball was dropped from in order to observe the rebound percentage later on. A person was required to drop the ball at certain heights: 20-200 cm, in increments of 20 cm. The ball’s initial height was recorded from the base of the ball at a given height; while observing videos after data collection, the ball’s rebound height was recorded, and then divided by the initial height to calculate the rebound percentage. A step ladder was used for heights that could not be reached in order to conduct data collection.

 

Materials: This experiment included the use of a bouncy ball, two meter sticks, video camera, stepstool, and tape.

 

Diagram:

 

Results:

 

In order to calculate the percent rebound of the bouncy ball for each given height, the rebound height of the ball was divided by the initial height of the ball (drop height). The results of the lab demonstrated that as the heights from which the bouncy ball was dropped from increased, so did the rebound percentage; the graph shows a positive correlation. The standard deviation was calculated for each average value to see how close the observed values were to the mean.

 

Data Table/Graphs:

 

Table 1: Effect of the Height (+/- 0.05cm) of Drop on Rebound Height (+/- 0.05%) - Raw Data
Trial #	Height of Drop (+/-   cm)
20	40	60	80	100	120	140	160	180	200
1	14.6	29.1	44.2	54.7	70.1	83.5	94.0	110.0	121.8	134.5
2	13.9	28.9	36.8	37.0	65.8	80.9	98.0	111.0	119.0	135.7
3	14.1	28.8	42.4	58.1	66.9	81.2	97.5	106.0	123.0	133.2
4	14.3	28.9	43.8	57.0	68.8	80.0	95.0	106.5	120.3	136.1
5	14.2	29.5	43.7	38.9	69.5	76.8	97.8	109.9	122.1	137.2
Average	14.2	29.0	42.2	49.1	68.2	80.5	96.5	108.7	121.2	135.3
Standard Deviation	0.3	0.3	3.1	10.3	1.8	2.4	1.8	2.3	1.6	1.5

 

Table 2: Effect of the Height (+/-0.05cm) of Drop on Rebound Percentage (+/-0.05% )
Trial #	Height of Drop (+/-0.05cm)
20	40	60	80	100	120	140	160	180	200
1	73.0	72.8	73.7	68.4	70.1	69.6	67.1	68.8	67.7	67.3
2	69.5	72.3	61.3	46.3	65.8	67.4	70.0	69.4	66.1	67.9
3	70.5	72.0	70.7	72.6	66.9	67.7	69.6	66.3	68.3	66.6
4	71.5	72.3	73.0	71.3	68.8	66.7	67.9	66.6	66.8	68.1
5	71.0	73.8	72.8	48.6	69.5	64.0	69.9	68.7	67.8	68.6
Average	71.1	72.6	70.3	61.4	68.2	67.1	68.9	67.9	67.4	67.7
Standard Deviation	1.3	0.7	5.1	12.9	1.8	2.0	1.3	1.4	0.9	0.8

 

 

 

Data: Text .:. Excel 

 

Conclusion:

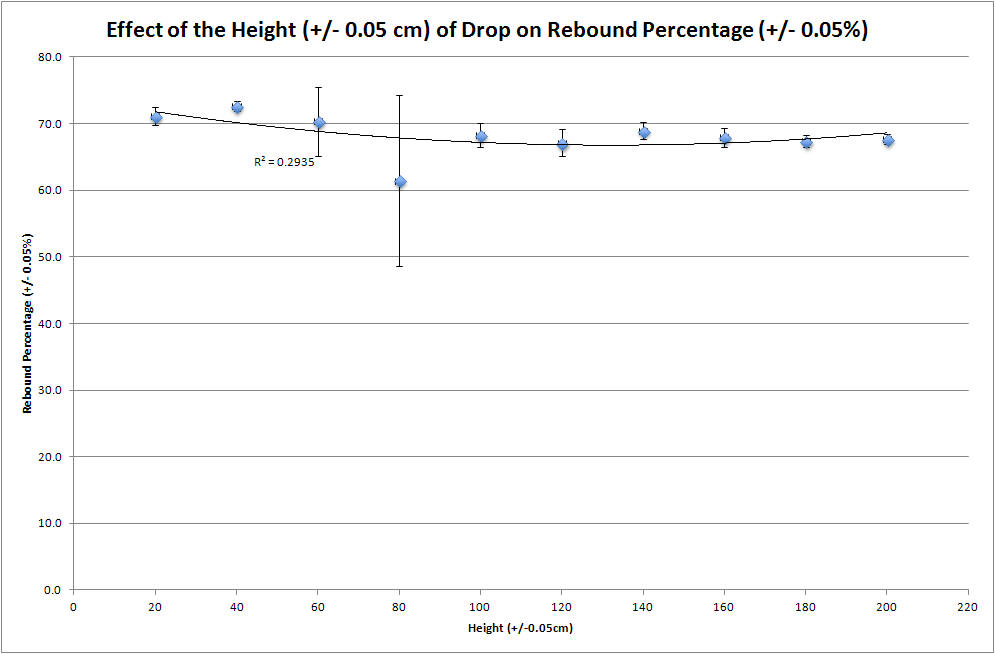
            The hypothesis states that if the height from which a bouncy ball is dropped is raised in increments of 20cm, respectively, from 20cm-200cm, then the bouncy ball dropped from 200cm will exhibit a greater rebound percentage. The results of the experiment come to the conclusion that as the height of the drop was increased, the percent of that height that the ball percentage of energy lost for each drop, regardless of height. This number was about seventy percent.

            In an ideal situation, 100% of the energy would have been conserved (Conservation of energy), meaning that the ball would have bounced back to the height it was originally dropped at. However, due to air friction, the ball lost energy on the way to the ground. Also, the collision between the ball and the ground is not elastic, meaning that not all energy is conserved. Due to these two factors, some energy is lost, resulting in the ball bouncing back to 70% of its original height, rather than 100%.

            Possible errors could come from many places. The height that the ball was dropped at might not have been precise and the height that was recorded for the rebound might not have been precise, because these two values were established with the eye, which is not 100% accurate. A major source of error, though, was that the ball didn’t always bounce back completely vertically. This was particularly apparent in the second and fifth drops at 80 cm, as seen with the large error exhibited on the graph in comparison with the other heights. These two drops went far to the side of the initial drop, meaning that a lot of energy was put into sideways motion rather than vertical motion. This results in flawed calculations, because we didn’t account for lateral movement.

            There are many improvements that could be made to this lab. One would be having the same person drop the ball each time, because that would be one less variable to account for. Another improvement would be to have some kind of restraint (like a tube) to drop the ball through, keeping it from bouncing to the side. Also, using a mechanical method of measuring height would have been much more precise.

 

Bibliography:

 

"Bouncing Ball Physics." Real World Physics Problems. N.p., n.d. Web. 09 Jan. 2015.

    <www.real-world-physics-problems.com/bouncing-ball-physics.html>

 

This website talks about bouncing ball physics, which demonstrates several interesting dynamics principles in conjunction with acceleration, momentum, and energy. Various principles will be discussed.

 

Science, Simple. Why Do Rubber Balls Bounce? (n.d.): n. pag. Why Do Rubber Balls Bounce? The

    University of York. Web.

    <www.york.ac.uk/media/cll/documents/rubberbounce.pdf>

 

This website give various reasons as to why rubber balls bounce. Specifically, it discusses what makes rubber so different to other non-elastic materials in reference to elasticity of a bouncing rubber ball.

"SuperBall History - Invention of the SuperBall." SuperBall History - Invention of the SuperBall. N.p., n.d.

    Web. 05 Nov. 2014.

    <www.wham-o.com/brands/superball.html>

 

This website gives a brief history of the wham-o superball.