1.) Introduction
2.) Method
3.) Results
4.) Conclusion
5.) Related Websites
6.) Bibliography
Ben Paul, Evan Kaeding, Sean Harrison, Jarod Peters
Pong 2.0
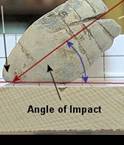If there is
a relationship, how does the angle of impact effect the velocity of a ping pong
ball shot at a sturdy wood block? The difference between speed and
velocity is key to our research project. Speed is simply how fast an
object is moving, whereas velocity is the speed and the direction that the
object is moving. Therefore the velocity of a projective can be negative,
but the speed will always be greater than or equal to zero. We are
testing how the angle of impact affects the velocity before and after the
impact. As the potential energy increases the velocity will increase as
well. Based on the formula Ek=1/2mv2 it does not
matter it the velocity is positive or negative because once it is squared it
will become a positive factor. Velocity is the only variable in the
equation because the ½ is a constant and the difference in the masses of the
ping pong balls is small enough to be neglected (and therefore a constant) velocity
is the only variable. Since the velocity is the only factor
affecting the kinetic energy it is possible to focus on the velocity because
the constants are going to affect each of the test the same. ÒThe angle
of impact is the acute angle between the tangent to the trajectory at the point
of impact of a projectile and the plane tangent to the surface of the ground
target at the point of impactÓ (Dictionary). The angle of impact is never
going to be more than 90¡ and because it would be negative the positive
angle. We predicted that the most energy loss will because the ping
pong ball should theoretical hit the wood board a perpendicular to its
velocity. Also we predict that the ping pong balls shot at a smaller
angle will maintain most of their initial velocity. We hypothesize that
if the angle of impact has an effect on the velocity of a ping pong ball shot
at a wooden board that as the angle of impact decreases the ping pong ball will
maintain most of its velocity. Our independent variable is the
angle of impact and our dependent variable is the velocity of the ping pong
ball. Our controlled variables include, but are not limited to the ping
pong balls, the camera, the table used as a base, the lighting of the
environment, ruler used to show path, same shooter.
Our materials included: a small piece of wood, a video camera, lights, yard stick, duct tape, right angle triangle with many angles marked on it, wood clamps and ping pong balls and a ping pong ball gun. We began our process by creating a sturdy and flat panel to shoot the ping pong balls at with the ping pong ball gun. The brace was positioned perpendicular to the edge of the table with straight edges. This brace was secured with wood clamps to the edge of the table. Because the angle of impact is measure as the angle between the path of the ball and the brace we used a right triangle marked with different angles to find the angle. Next we taped the a thin metallic yard stick to the table to provide a line of sight for Sean, the shooter, and it also provided a nice reference point when using analysis the video in Logger Pro. The last step before shooting the gun is setting up the camera. The camera was positioned directly above the impact site. The camera was recording at 120 frames per second, requiring an inordinate amount of light for a clear shot. Finally we shot the ball at different angles to test the effect of the angles of impact on the velocity. As seen in the image the ping pong ball shooter is aligned along the yard stick which has been set at our current test angle. We chose to test angles of impacts in intervals of 10. We tested 10, 20, 30, 40, 50, 60, 70, 80 and 90 degrees.
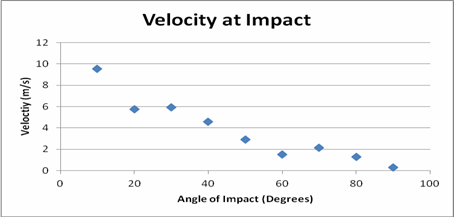
Our calculation was simply an application of geometry. Because we had the camera overhead we were able to use the Pythagorean Theorem to account for the X and Y velocities and find the vector component velocity. The percent conserved is simply the finial velocity over the initial velocity multiplied by 100.
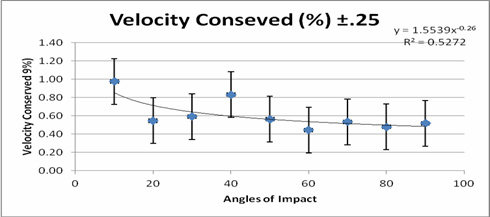
This graph above illustrates the percent of the velocity conserved. The velocity is conserved more as the angle decreases, but it is not uniform. The R2 coefficient is only .538 so the trend line is not represented by any line very effectively.
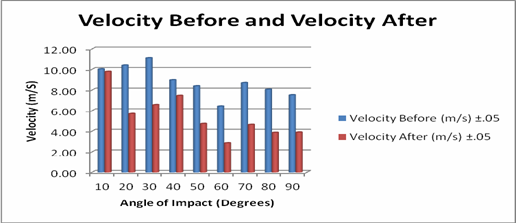
The bar graph is an excellent visual for the effect of the impact. As the angle increases the velocity is a smaller and smaller percentage of the initial velocity.
This is the most interesting graph for us. As the angle of impact decreases it becomes harder and harder to determine a velocity near the impact site. This site shows the closest velocity we were able to record on Logger Pro. So, as the angle of impact increases we were able to get a data point close and closer to no velocity. We know that for one moment the y component velocity must be zero because of the Intermediate Value Theorem, that states if a function goes from positive to negative or vice versa, it must pass through zero. The fact that our equipment was unable to show this change is a testament to its ineptitude.
Our results seem to indicate that the angle of impact seems
to have an effect on the amount of energy conserved. This cannot be
confirmed due to the variance in our data, but we think that it is very likely
to be true. Also, the data aligns with our hypothesis that the bigger
angles of impact will have a greater effect on the velocity. The graphs
are trending down, but due to the seemingly random nature and significant error
of each point there is no way to tell for sure without further testing. I
think that the data turned out as it did because the as the angle of impact
increases the vector of the ball is becoming more and more into the
plane. When the ball is nearly flush with the plane only a small part of
the vector is into the plane and therefore less energy is transferred into the
plane leaving the balls velocity higher. Our largest source of error was
accounting for the speed of the ping pong balls. The ping pong balls were
moving close to nine meter per second in most cases. Even with a camera
shooting 120fps they we could manage to capture around 5 frames of reliable
data. Also, keeping the gun stable while shooting at the board was a
challenge for Sean. He did a swell job, but the gun must be pumped and
this motion caused him to slightly alter the trajectory of the ball. If
we were to do this lab again we would use a camera that shot significantly more
frames per second. Also, we would have a better camera finding some way to control
the gun without compromising its function would help. Bracing the gun
would be an option as long as it did not interfere with its
firing.
1.) http://physiology.umc.edu/themodelingworkshop/Model%20Library/Bouncing%20Ball/Bouncing%20Ball.HTML
-This website discusses the fundamental principles of how distance and angle of impact affects the velocity.
2.) http://hyperphysics.phy-astr.gsu.edu/hbase/traj.html
-This website discusses the formulas involved in determining the distance and angle pertaining to the velocity of the ball when striking some surface.
3.) http://www.sciencedirect.com/science/article/pii/S0734743X01001105
-This discusses a similar procedure carried out to determine whether impact velocity affects the striking surface more than the angle of impact.
4.) http://www.golf-simulators.com/physics.htm
-The physics of a golf ball pertain to a high degree to the determined position and velocity when given different striking points and angles.
5.) http://www.racquetsportsindustry.com/articles/2004/04/follow_the_bouncing_ball.html
-This website goes in depth to further explain the physics of spherical objects and their trajectory based on several different factors such as angle of impact.
"Conservation of Momentum -- from Eric Weisstein's World of Physics." ScienceWorld. Web. 27 Jan. 2012. <http://scienceworld.wolfram.com/physics/ConservationofMomentum.html>.
Dictionary.com | Find the Meanings and Definitions of Words at Dictionary.com. Web. 27 Jan. 2012. <http://dictionary.reference.com/>.
Giancoli, Douglas C. Physics: Principles with Applications. Upper Saddle River, NJ: Pearson/Prentice Hall, 2009. Print.
Stewart, James. Single Variable Second Edition Calculus Concepts and Contexts. Pacific Grove, CA: Brooks/Cole, 2001. Print.
Tabe