:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
______ ____ ____ __ ____ ____ ______ ____ __ ______ ____
/'\_/`\ /\ _ \ /\ _`\ /\ _`\ /\ \ /\ _`\ /\ _`\ /\ _ \ /'\_/`\ /\ _`\ /\ \ /\ _ \ /\ _`\
/\ \\ \ \ \ \\ \ \ \ \\ \ \ \ \\ \ \ \ \ \ \_\ \ \ \ \ \\ \ \ \ \ /\ \\ \ \ \ \ \ \ \ \ \ \\ \\ \ \ \ \
\ \ \__\ \\ \ __ \\ \ , / \ \ _ <'\ \ \ __\ \ _\ \ \ , / \ \ __ \\ \ \__\ \\ \ ,__/ \ \ \ __\ \ __ \\ \ _ <'
\ \ \_/\ \\ \ \/\ \\ \ \\ \ \ \ \ \ \\ \ \ \ \\ \ \ \ \ \ \ \\ \ \ \ \/\ \\ \ \_/\ \\ \ \/ \ \ \ \ \\ \ \/\ \\ \ \ \ \
\ \_\\ \_\\ \_\ \_\\ \_\ \_\\ \____/ \ \____/ \ \____/ \ \_\ \_\\ \_\ \_\\ \_\\ \_\\ \_\ \ \____/ \ \_\ \_\\ \____/
\/_/ \/_/ \/_/\/_/ \/_/\/ / \/___/ \/___/ \/___/ \/_/\/ / \/_/\/_/ \/_/ \/_/ \/_/ \/___/ \/_/\/_/ \/___/
by Andrei Flores, Naoki
Minato, and Jimmer shen
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
:Introduction::Method::Result::Conclusion::Bibliography::Go Up:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Introduction
The inquiry for this lab is
based off of how the efficiency in which a curved ramp converts potential
energy into kinetic energy can be increased. This lab is an adaptation of a lab
where a flat ramp would be used to predict the velocity of a marble by timing it's
time over a distance and finding its velocity, then determining the kinetic
energy it exerts as it exits the ramp. Since we're dealing with energy, we can
eliminate the uncertainty of time by using projectile motion equations to solve
for time and final horizontal energy exiting the ramp instead. An important
principle for this lab is Conservation of energy which states that the total
energy in a closed system remains constant (source 2). From this concept,
energy equations were derived to form potential energy and kinetic energy
equations based off of the concept of force over a certain distance. In order
to examine the efficiency of a ramp converting vertical potential energy into
horizontal kinetic energy, one would simply find the difference of energy, or
work, from the beginning to the end of the process and compare the results to
the changes made to influence those changes. In this case, its the length of
the tube.
In this lab, we will be rolling the marble off of the end of a table in order
to use projectile motion equations to help find final horizontal kinetic energy
as the marble leaves the ramp. Why does this work? Well, projectile motion
equations are derived from the different differentiations of the graph
velocity/time, which help determine displacement, initial velocity, final
velocity, acceleration, and change in time of an object in motion in their
individual vectors. By using their relationships, the displacement equations,
S=(u)(t)+1/2(a)(t)^2 and (v)^2=(u)^2+2(a)(s), was found (Source 4). We will be
using this equation later on to help calculate energy.
Problem:
How does the
length of a ramp affect the work needed to change potential energy to
horizontal kinetic energy of a marble exiting the ramp?
Hypothesis:
If the length of
the ramp decreases, then the horizontal velocity exiting the ramp will
increase. Therefore, the work decreases and more energy is conserved.
Variables:
Independent
Variable: Length of ramp (meters),
Dependent
Variable: Horizontal velocity (meters/second)
Controlled: Height
of table and tube (meters)
:Top:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Method
In preparation for the lab, it is recommended to work in indoors where there is a large area with a leveled wooden or tiled floor. Materials that are required for the experiment include a flat table at least one meter long, a plastic tube with a smooth inner and outer surface thats roughly 1 meter long, at least three different massed smooth surfaced marbles, a ring stand, two meter sticks, carbon paper, a roll of tape, an eraser, and a sharp cutting tool.
We taped the end of the tube to the top of the ring stand and the other side of the tube to the end of the table. Take measurements of the height of the table, the height of the entrance to the tube, length of the tube, and the horizontal distance from the end of the tube to the entrance. Lay the carbon paper onto the floor at the end of the table until roughly a meter away with no exposed surface area of the floor. Make sure that the tube is cleaned and not bent in any spots, as this will affect the consistency of the experiment. Take a marble and line it up with a ruler at the entrance so that its at the same exact height as the tube. Release the marble and once the Marble lands on the carbon paper, it will leave a mark which indicates the distance of the impact using a meter stick (Dont forget to erase previous marks so that its easier to indicate where the marble had landed).
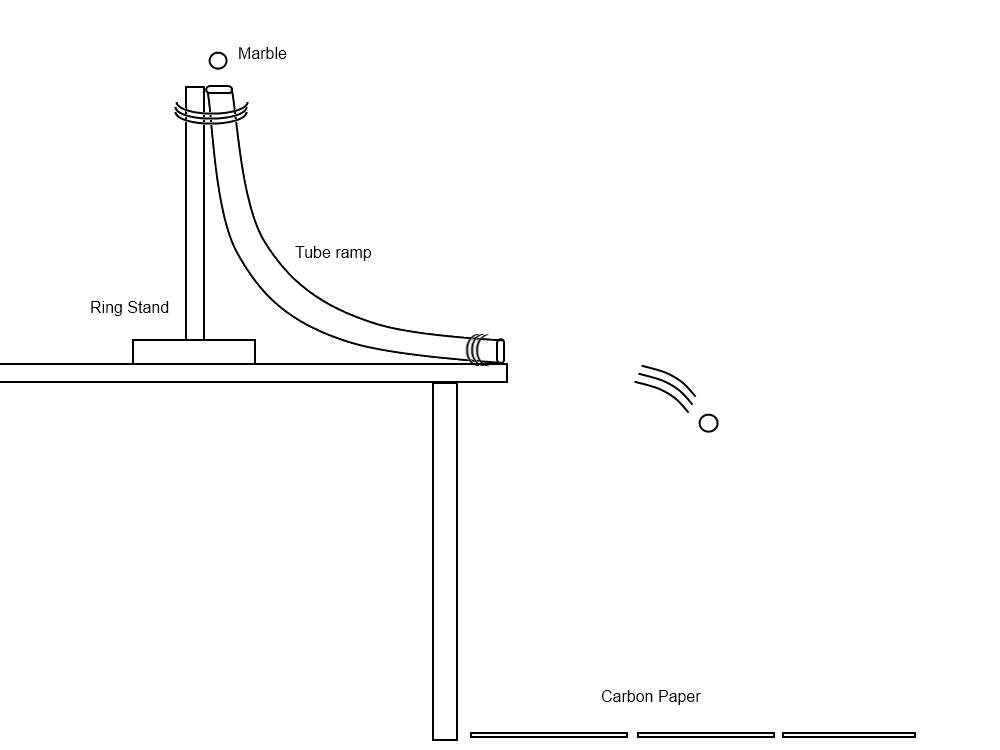
We tested 5 different lengths of the tube (127 cm, 122cm, 117cm, 112 cm ,and 107cm) by cutting 5 cm off of one end at the end of each trial and repositioning it next to the edge by 5 cm. We also tested with 3 different marbles (5 trials each) with different weight and materials for different amount of energy transfers (Shiny Marble weight 8.41 g, Heavy metal weight 14.59g, and clear marble weight 3.32g). It is recommended to use multiple meter sticks to line up the end of the table with a meter stick perpendicular to it on the floor as a reference point when measuring the horizontal distance traveled by the marble. It is also recommended that smooth marbles be used in this lab, as it can alter the results of this experiment.
:Top:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Results
In our investigation, we obtained 5 different lengths with 3 different marbles, 5 trials each marble for each tube length.
|
Length of tube=127cm |
|
ramp distance=91cm |
ramp distance=86cm |
ramp distance=81cm |
ramp distance=76cm |
ramp distance=71cm |
|
Marble |
Trial |
Distance from table ±0.5(cm) |
Distance from table ±0.5(cm) |
Distance from table ±0.5(cm) |
Distance from table ±0.5(cm) |
Distance from table ±0.5(cm) |
|
Shiny |
1 |
65.8 |
70.2 |
76.2 |
83.4 |
91.6 |
|
|
2 |
71.3 |
68.8 |
74.5 |
82.5 |
75.5 |
|
|
3 |
67.5 |
68.5 |
71 |
83.5 |
87.4 |
|
|
4 |
63.5 |
75.3 |
75 |
85.8 |
96.4 |
|
|
5 |
69.9 |
66.9 |
69.9 |
88 |
94.8 |
|
Heavy |
1 |
68.3 |
68.8 |
72.5 |
79 |
72 |
|
|
2 |
65.4 |
70 |
71.2 |
75.9 |
77.3 |
|
|
3 |
60.1 |
70.4 |
71.3 |
72 |
70.1 |
|
|
4 |
70.2 |
67.8 |
75.6 |
77.3 |
78.9 |
|
|
5 |
69.9 |
66.6 |
77.7 |
69.8 |
72.3 |
|
Clear |
1 |
49.6 |
53.1 |
52 |
69.8 |
54.5 |
|
|
2 |
50.4 |
57.8 |
65.4 |
41.7 |
70.2 |
|
|
3 |
58.5 |
52.5 |
55.6 |
58.2 |
67.9 |
|
|
4 |
58.7 |
58.8 |
54.7 |
57.3 |
51.3 |
|
|
5 |
53.3 |
52.8 |
52.2 |
61 |
63.8 |
|
Marble Type |
Length of Tube ± 0.5(cm) |
Average Distance Traveled |
Uncertainties ± (cm) |
|
Shiny |
127 |
67.6 |
3.9 |
|
|
122 |
69.94 |
4.2 |
|
|
117 |
73.32 |
3.15 |
|
|
112 |
84.64 |
2.75 |
|
|
107 |
89.14 |
10.45 |
|
Heavy |
127 |
66.78 |
5.05 |
|
|
122 |
68.72 |
1.9 |
|
|
117 |
73.66 |
3.25 |
|
|
112 |
74.8 |
4.6 |
|
|
107 |
74.12 |
4.4 |
|
Clear |
127 |
54.1 |
4.55 |
|
|
122 |
55 |
3.15 |
|
|
117 |
55.98 |
6.7 |
|
|
112 |
57.6 |
14.05 |
|
|
107 |
61.54 |
9.45 |
[ Text /
Excel ]
The data is averaged
and graphed according to the length of the tube.
More data
collected...
|
Marble: |
Shiny |
Heavy |
Clear |
|
Mass (g) ±0.005 |
8.41 |
14.59 |
3.32 |
|
|
Height ± 0.5(cm) |
|
Table |
67.5 |
|
Ring Stand |
61 |
4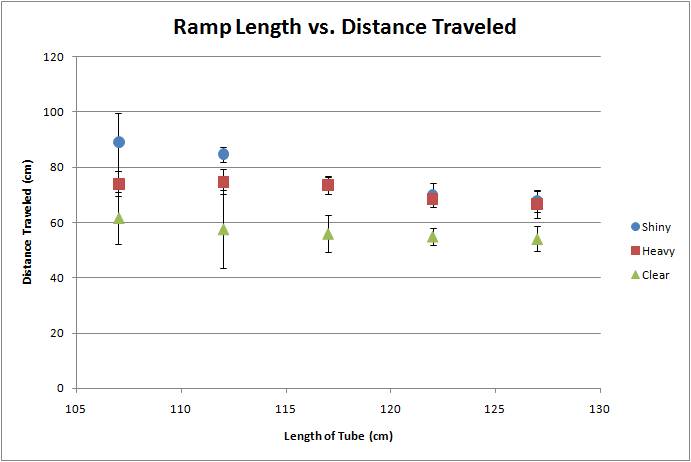
Error bars are found using (high-low)/2 for each individual average.
According to the relationship between ramp length and distance traveled, we can discover that there is some correlation between the ramp length and the final kinetic energy. To further investigate this relationship, we compare the formulas:
Potential Energy = Mass*Gravity*Height(ring stand)
and
Kinetic Energy = ½*Mass*Velocity^2
First, Downward
Potential Energy(making sure to convert to meters)....
|
Marble Type |
PE (J) |
|
Shiny |
50.32 |
|
Heavy |
87.30 |
|
Clear |
19.86 |
Now to solve for Kinetic energy, we must use the previously stated vector equations:
S=(u)(t)+1/2(a)(t)^2
and
(v)^2=(u)^2+2(a)(s)
Where gravity = 9.81 m/s/s, downward
Stable=0*t+1/2(9.81)(t)^2
t=(2*.675/9.81)^1/2
time=.3709s
Now using the average distances, we find final velocity of the horizontal vector...
S=u*.3709
u=S/.3709
Since (v)^2=(u)^2, then final velocity equals initial velocity. Now we convert to energy using:
KE=1/2(m)(v)^2
|
Marble Type |
Length of Tube ± 0.005(m) |
Horizontal Vfinal (m/s) |
Kinetic Energy (J) |
V Uncertainty (m/s) |
KE Uncertainty (J) |
|
Shiny |
1.27 |
1.82 |
13.97 |
13.97 |
101.53 |
|
|
1.22 |
1.89 |
14.95 |
14.95 |
108.69 |
|
|
1.17 |
1.98 |
16.43 |
16.43 |
119.45 |
|
|
1.12 |
2.28 |
21.90 |
21.90 |
159.18 |
|
|
1.07 |
2.40 |
24.29 |
24.29 |
176.56 |
|
Heavy |
1.27 |
1.80 |
23.65 |
23.65 |
171.96 |
|
|
1.22 |
1.85 |
25.04 |
25.04 |
182.04 |
|
|
1.17 |
1.99 |
28.77 |
28.77 |
209.15 |
|
|
1.12 |
2.02 |
29.67 |
29.67 |
215.68 |
|
|
1.07 |
2.00 |
29.13 |
29.13 |
211.77 |
|
Clear |
1.27 |
1.46 |
3.53 |
3.53 |
25.67 |
|
|
1.22 |
1.48 |
3.65 |
3.65 |
26.53 |
|
|
1.17 |
1.51 |
3.78 |
3.78 |
27.49 |
|
|
1.12 |
1.55 |
4.00 |
4.00 |
29.10 |
|
|
1.07 |
1.66 |
4.57 |
4.57 |
33.22 |
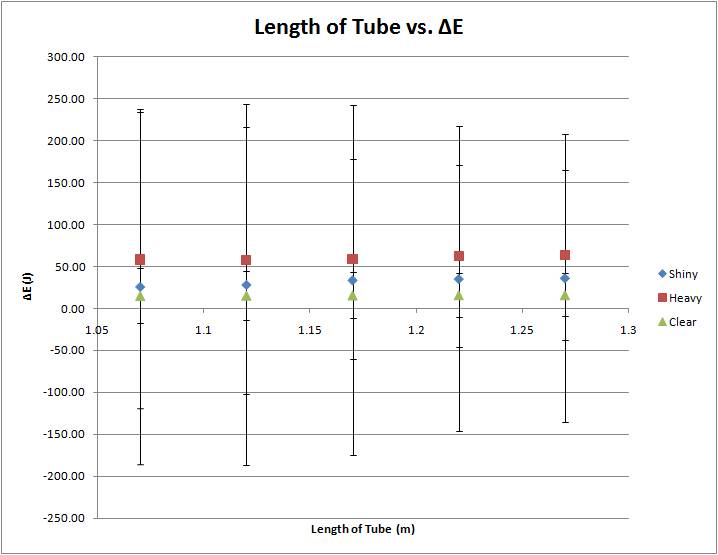
ΔE=( Potential - Kinetic )
|
Marble Type |
Length of Tube ± 0.005(m) |
ΔE (J) |
ΔE Uncertainty (J) |
|
Shiny |
1.27 |
36.36 |
101.53 |
|
|
1.22 |
35.37 |
108.69 |
|
|
1.17 |
33.89 |
119.45 |
|
|
1.12 |
28.43 |
159.18 |
|
|
1.07 |
26.04 |
176.56 |
|
Heavy |
1.27 |
63.66 |
171.96 |
|
|
1.22 |
62.27 |
182.04 |
|
|
1.17 |
58.54 |
209.15 |
|
|
1.12 |
57.64 |
215.68 |
|
|
1.07 |
58.18 |
211.77 |
|
Clear |
1.27 |
16.34 |
25.67 |
|
|
1.22 |
16.22 |
26.53 |
|
|
1.17 |
16.09 |
27.49 |
|
|
1.12 |
15.86 |
29.10 |
|
|
1.07 |
15.30 |
33.22 |
:Top:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Conclusion
According to the results without the margins of error, the shorter the tube, the further the marble travels from its origin. Therefore, requires a higher velocity exiting the tube as well as maintaining a higher kinetic energy. To conclude, the shorter the tube, the less change in total energy there is within the system, resulting in a more efficient ramp.
This data supports our thesis that the shorter the length of the ramp is, the higher the kinetic energy is when leaving the system. This works because the height remains constant so the potential energy will be constant also. Therefore, our project tests the acceleration of the marble in relation to the distance it travels in the tube. This allows us to determine the efficiency of the ramp without having to use rocket surgery.
However, when the error bars are taken into account, all these patterns could be inconclusive due to the severity of its range. One source of errors could stem from the drag resistance, which could change the results. However, since the marbles are all relatively similar in size, its really negligible when determining the correlation between the energy before and after the ramp. Other major sources of error could come from the quality of the tube ramp, friction from rolling inside the tube because the velocity decreases, and the smoothness of the marbles surface. By acknowledging these variables, we can further improve our procedure by improving on what was just stated, as well as a better method of holding down the tube, having a recorder to use logger pro for more accurate measurements, and different sizes of tubing.
The inconsistency of the results leads us to believe that there may or may not be any relationship whatsoever because the error bars on the length of tube vs distance traveled graph are just as inconclusive as the change in energy graph.
:Top:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Bibliography
1.8. THE
CONSERVATION OF ENERGY
Explains conservation of energy with respect to kinetic energy and potential
energy.
2.What Is
Potential Energy
Exmaples of how P.E. equations work.
3.
KINETIC ENERGY-K.E
= 1/2 Mv2
Equations for Kuinetic Energy.
4. Physics For Idiots - Dynamics
Explains S.U.V.A.T.
Applies to both the marble and the ramp.
:Top:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::