Physics Research Project
The Tennis Ball Slingshot of Death
By
Grant Hughes, Laurel Vandehey, Tegan Valo, Alison Stone
Section
Background
The most common use for a slingshot today is for entertainment, from wreaking havoc in the household to killing squirrels in your backyard (History). For this experiment, we ramped up the dimensions of the slingshot and used it for science!
There are so many different variables that are involved with the use of the slingshot. Our group is interested on the effect mass has on the distance the slingshot shoots objects. Although there are horizontal and vertical distances affected by the mass, we are only interested in the horizontal distance the ball travels. The band being used follows the spring constant rule, which is F=kx (k being the spring constant and x being the distance pulled back) (TuHS). The more one pulls it back, the more force applied to the ball.
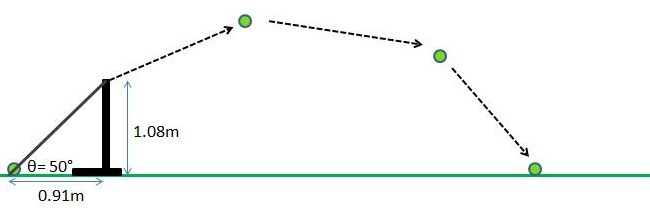
We are using a tennis ball and adding BB's into the center of it. We will then shoot it from a controlled distance of .9144 m back and at a 50° angle every time. We then will do five trials at each mass (16 variations) in order to get the most accurate answer. The dependent variable will be the distance the tennis ball travels; we assume that this will change as the mass changes. The independent variable will be the combined mass of the tennis ball and the added BB’s. The controlled variables include, but are not limited to, the ball’s mass and size, the air and wind (hopefully), the angle of trajectory, the person releasing the ball, the slingshot and the distance the slingshot is pulled backwards and downwards.
Statement of the Problem
“The purpose of this experiment is to find how the relationship between the mass of a ball to the horizontal distance the ball travels in the air.”
Hypothesis
“We believe that the distance traveled by the tennis ball will increase as the mass of the tennis ball increases. We believe that this will occur because the ball will have more energy due to its increased mass.”
Bibliography
Douglas C. Giancoli. Physics: Principles with Applications(italics). New Jersey. Pearson Prentice Hall, 2009. Print.
"History of the Slingshot." Blog. The Warriors Club. WordPress, 6 Aug. 2011. Web. 28 Oct. 2011. <http://the-warriors-club.com/2011/08/history-of-the-slingshot/>.
"Mass of a Tennis Ball" The Physics Factbook. Glenn Elert. Thur. 12 Jan. 2012. <http://hypertextbook.com/facts/2000/ShefiuAzeez.shtml>
“Tualatin Physics” TuHS Physics Homepage. Web. 28 Oct. 2011. http://tuhsphysics.ttsd.k12.or.us/
"The Uncertainty Principle" Stanford Encyclopedia of Philosophy. Jan Hilgevoord. Mon. 8 Oct, 2001. Thur. 12 Jan, 2012. <http://plato.stanford.edu/entries/qt-uncertainty/>
We tested the effect of mass (BB’s) added to a tennis ball on the distance in which a slingshot can shoot it. Because there are many variables in using a slingshot, such as the spring constant of the band, the distance that it is pulled back before releasing, and the angle at which it is pulled, we created a makeshift slingshot apparatus that has crossbars and is stable. We pulled the tennis ball all the way back 50° to a hash-mark located .9144m from the 1.08m tall posts every single trial. These were our control variables; hopefully these precautions made the data we collected as consistent as possible. Once the tennis ball was pulled back and released, we watched carefully where it landed. The horizontal distance traveled will be measured from the bottom of the slingshot to the point where the ball initially hits the ground. We measured the distance traveled using the hash-marks on the field (because the experiment took place on a football field) and then used a meter stick to specify the exact distance (we had to convert the yards to meters). We then recorded the distance and repeated the trial. To alter the tennis ball’s mass, we cut a small slit into the ball, 2cm long, to place BB’s into the ball. We measured the mass of the tennis ball and the mass of 10 BB’s. The tennis ball had a mass of 55g and the 10 BB’s had a total mass of 4g. We did five trials of sixteen variations of mass (grams): (55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 103, 111, 119, 127 and 135). The different masses added to the tennis ball (even though they seem small) should create a small change in the distance the ball travels, whether the distance traveled increases or decreases.
Materials
· Tennis ball
· Knife (to cut hole in ball)
· Slingshot (with elastic bands)
· 200 BB’s
· Meter stick
· Supplies to record data
|
Calculus (finding the ideal mass):
f(x)=-.0012x2+.2384x-0.7231
f'(x)=-.0024x+.2384
0=-.0024x+.2384
x≈99.33g
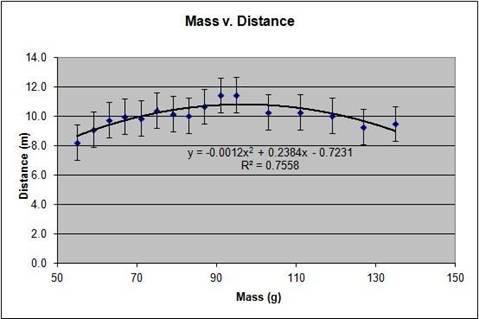
As one could see by the XY scatter-plot, the shape of the data resembles a parabola. This shows that with less mass, the ball travels less distance while the added mass adds to the distance traveled. Once the ball surpasses its “ideal mass,” the distance begins to decrease. Our ideal mass of a tennis ball is about 99.33g. This would give us a distance of 11.12m.
As one could see by the XY scatter-plot, the shape of the data resembles a parabola. This shows that with less mass, the ball travels less distance while the added mass adds to the distance traveled. Once the ball surpasses its “ideal mass,” the distance begins to decrease. Our ideal mass of a tennis ball is about 99.33g. This would give us a distance of 11.12m.
Our hypothesis was half correct. With the increase of mass, we did see an increase in the distance the ball traveled. But, somewhat not surprisingly, the distance started to decrease at a certain mass as we added more BB’s to the ball.
The results occurred the way they did because of a few factors. First of all, the tennis ball variations with lower mass didn’t shoot as far because they had less inertia, resulting in a low resistance to air friction. With a smaller amount of mass, the tennis ball has less energy (Ek=.5mv2 & Ep=mgh) to resist the friction. Air resistance occurs when an object moving in the air creates friction with the air, slowing it down. When the mass increased, the air friction had less of effect on the ball because the ball had more energy and inertia. After a certain mass (99.33g), the tennis ball began to fly a shorter length of distance. This is because the ball became too heavy for the slingshot band. With the smaller mass, the ball was fighting the slingshot. With the heavier mass, the slingshot was fighting the ball. These factors resulted in a parabola-shaped graph with the smallest and heaviest masses on the lower ends.
One of the main sources of error was the slingshot itself. It was a very inaccurate slingshot; the balls would sometimes shoot out incorrectly from the sling due to the sling itself, or human error. This played a large role in the inconsistencies of the data. The uncertainty of the data (±1.2m) is relatively large. Another source of error, though it may be small, is measuring the mass of the ball and the BB’s. We used a regular scale to measure the masses, but it only measured to the nearest gram.
There were many things we could improve on in this experiment. One could be to take more trials. Some of our values for each mass differed greatly; with more trials, we could have a more precise average. Another would be to have more variations in mass. The more data points on the graph, the better the trendline for the data will be. The place we did the experiment could also be improved. There was definitely some wind affecting the ball’s trajectory. Performing this in a closed air building (a gym) would ensure that wind would not be a factor. The main thing that would be changed is the slingshot itself. Stated above, it did not provide accurate data. The slingshot was inconsistent, which was probably our main source of error. To improve this, we would use a real slingshot with a pouch that would hold the ball and improve the consistency of each shot.
Tennis Ball Slingshot of Death Presentation
Simply watch this expertly crafted presentation for a simpler understand of this project.
General Relativity and Slingshots
An interesting article about Einstein's General Theory of Relativity. Students from Purdue University use gravitational forces to test Einstein's theory.
Transfer of Energy with a Slingshot
Demonstrates and explains the energy transferred from the elastic slingshot to the projectile.
An interesting documentary explaining the physics of slingshots, some of it's history and just some really cool stuff.
The newest version of Angry Birds needed the help of physicists to be created. Describes the process of designing a realistic game with birds in slingshots.