An Examination of the Relationship between the Percentage of Water to Corn Syrup and Resonant Frequency

Nathan Gardner

Becka Kasten

Rebecca Albertson


Table of Contents

Introduction

Method

Results

Diagram

Graph

Conclusion

Work cited

Return to IB 2012

Introduction

 

Background Information:

            We are all familiar with making a wine glass “sing.” Simply drag a wet finger around the edge of a crystal wine glass, and a pure note resonates through the air. “In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others” (Resonance, Wiki). When a vibrating system is set into motion, it vibrates at its natural frequency. When an outside force is applied to a system, this results in a forced vibration. This effect is known as resonance, or resonant frequency. In simpler terms, when you drag your finger around the edge of a wine glass, it is causing a forced vibration which results in the “singing” or resonant frequency that is heard. Dragging your finger on the rim creates friction, which then causes the glass to vibrate and create resonance.

Adding liquid to the glass can change the pitch of the resonant frequency. The sound wave of the resonant frequency moves the molecules of the liquid around the glass making, in essence, small waves. These small waves decrease the energy of the sound wave which in turn lowers the pitch of the frequency that is heard. Because different liquids are denser than others, we can assume that variations on the density of liquids would produce different pitches.

 

Question: The purpose of this experiment is to find out how different variations of water and corn syrup (different densities) affect the resonant frequency of a wine glass.

 

Hypothesis: If denser liquids absorb more energy, then when different variations of water and corn syrup are put in the same wine glass, the variations with a higher concentration of corn syrup will cause the wine glass to produce a lower resonant frequency than that of the variations with a higher concentration of water. The variations of water and corn syrup represent the independent variable while the frequency is the dependant variable. The controlled variables include the wine glass, the measurement of the liquids and the temperature of the room.

 

Method


Materials:



Procedure:
           First, place ½ a cup of water in the wine glass. When measuring, fill the measuring cup all the way so that the water/corn syrup creates a meniscus. Then, after slightly wetting a finger, drag it around the rim of the glass till it produces a “singing” tone. Using the electric tuner, find the resonant frequency by holding the tuner next to the singing glass. At least five trials were taken in order to find an accurate reading of the resonant frequency. Clean the glass out after each variation. Repeat this procedure with the different variations of water vs. corn syrup. For example, we used five different variations: 100% water, 75% water-25% corn syrup, 50% water-50% corn syrup, 25% water-75% corn syrup, 100% corn syrup.

 

 

Results

 

 

Trial number

100% water; 0% corn syrup

75% water; 25% corn syrup

50% water; 50% corn syrup

25% water; 75% corn syrup

0% water; 100% corn syrup

1

810.5

807.1

806.3

798.5

794.0

2

809.7

807.0

806.7

798.0

793.3

3

808.4

806.5

806.9

797.9

793.9

4

809.4

806.8

805.9

799.0

794.1

5

809.0

807.2

805.7

799.2

793.9

average

809.4

806.9

806.3

798.5

793.8

Data File: Text .:. Excel


Diagram

Graph

 

Data File: Text .:. Excel

 

 

 

 

 

 

Conclusion

 

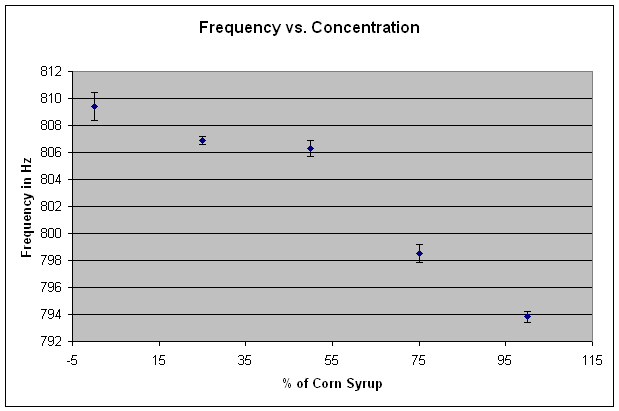
The results of our research experiment are that, as the density of the solution increased, the resonant frequency the glass emanated decreased. While there was no steady correlation between the density and the frequency, it can be determined from the data collected that the overall frequency of each solution decreased, to some extent, as the percentage of corn syrup increased. The graph above demonstrates the general decline of the frequencies, where the average frequency of water was 809.4 Hz, and fell to 793.8 Hz for 100% corn syrup. In terms of our hypothesis, our prediction was accurate. Although the results weren’t as extreme as we hoped it would have been, the data collected still supports the hypothesis; the average frequency of each different solution decreased as more corn syrup was added. The formula to find the frequency is: f=1/2π√(m/k)

    Our explanation for why the frequency decreased is because as the density increased, the period of motion would also increase. As the period of motion increases, the resonant frequency decreases. The formula used to derive the frequency is f=1/T, where T is the period of motion, and f is the frequency.  The higher the density the harder it it, and consequently, the longer it takes, for sound waves to travel through the solution.

    In this research experiment, the main sources of error mostly stem from human error. The complete accuracy of the ratios of the solutions is most likely not completely accurate. Due to the fact that we utilized household measuring cups, the accuracy of the amount of water and corn syrup may vary. We measured it so that there was a slight overhang above the top of the measuring cup.


Works Cited

“CCMR-Ask A Scienctist!” Cornell Center for Materials Research. Web.19 Jan. 2012.

            <http://www.ccmr.cornell.edu/education/ask/index.html?quid=1143>. (Gave us useful information on how to best get resonance out of the glass and the mechanics of the process.)

“Frequencies of Musical Pitches.” People. Virginia.EDU. Web. 19 Jan. 2012.

            <http://people.virginia.edu/~pdr4h/pitch-freq.html>. (We learned the way in which sound is actually formed from the resonance of the wine glasses and the friction between glass and finger.)

Giancoli, Douglas C. Physics. Principles with Applications. Upper Saddle River, NJ:

            Pearson/Prentice Hall, 2005. Print.

“Light and Sound Waves.” Concordia College, Moorhead, Minn. – Concordia

            College-Moorhead, Minnesota. Web. 19 Jan. 2012.

            <http://www.cord.edu/faculty/manning/physics215/studentpages/angieevanson.html>. (Knowledge about how resonance works specifically with wine glasses and other objects.)

“Resonance.” Wikipedia, the Free Encyclopedia. Web. 24 Oct. 2011.

            <http://en.wikipedia.org/wiki/Resonance>. (This gave us a lot of general knowledge about resonance, and refreshed what we learned last year.)