WATER ROCKETS

By: Laura Romrell, Griffin Harger, and Justin Ross

[Return to Research Page | Background Info | Purpose  | Review of Literature | Hypothesis | Operational Definitions | Procedures | Data | Conclusion | Bibliography | Related Links]

Background Information: (Back to top)
A water rocket is exactly what it sounds like, a rocket that uses water as its counter mass to propel it through the air. The most commonly used form is a modified refreshment container, other wise known as a soda bottle. Water is propelled out of the bottom of the bottle by pressurized air encapsulated above the water in the bottle. The release of this air and water creates a counter thrust effect. The same basic principles between normal rockets and bottle rockets are the same (3). There are three main forces which control the direction of the rocket: thrust (flap), drag (Ffr), and weight (w=mg). The thrust is provided by the release of the reaction mass, which in this case is the water in the water rocket. This thrust occurs because of the difference in atmospheric pressure artificially created inside the water rocket when compared to the “natural surroundings” (4). The drag force exist because of the friction caused by air molecules along the side of the rocket (3).variance in the shape of the rocket will affect the amount of drag the rocket experiences, thus, because this is not the factor we wish to test, we will need to make sure this remain as constant as possible. Lastly weight is simple the mass of the rocket multiplied by gravity. In order for your rocket to launch, the thrust force must be stronger than its weight. The physics principal behind a bottle rocket works is Newton’s third law which states that for every action there is an equal and opposite reaction. This is essentially the same as when you push against a wall, you push and it pushes back. In our case the action is the mass of water being propelled down and out of the bottle by the air pressure, which in an opposite reaction propels the water rocket up. There are many possible factors to analyze for a bottle rocket, such as launch velocity, distance launched, air friction, parabolic arch, amount of water, shape of rockets, and launch angles are all possible factors to analyze. Things that could affect the experiment are changes in atmospheric pressure, temperature, changes in humidity, wind, and rain.
 


Purpose: (Back to top)
The purpose of this experiment is to find the relationship (independently and collectively) between the amount of water in the water rocket, the amount of pressure and the horizontal displacement.
 

Review of Literature: (Back to top)
When constructing our rockets there are 5 critical factors we must remain aware of. These are: reliability, rigidness, precision, weight, and drag. (2) Reliability refers to the consistency with which the rocket flies. This is important, because if there are huge discrepancies between the distances when all factors are left constant, our uncertainty value will be too high to be able to judge the impact of out independent variable. The second one, rigidness, Singleton (2) stresses is one of the most overlooked. If the rocket or any part of the fins is able to flex, there is no way to accurately calculate how it will perform in the air, and thus it is not reliable. Precision refers to the actual construction process. Again, Singleton stresses that even only one millimeter adjustment can affect whether your rocket is even able to take off. Weight will be one of out independent variables so we do not have to such great lengths to make sure every thing is equal, since it will be adjusted. Lastly drag will need to be constant on all our rockets and launches in order to obtain analyzable data (2).
 

Hypothesis: (Back to top)
Our hypothesis is three fold.
We believe that graphically (with mass as the independent variable and distance as the dependant) our results will resemble that of a bell curve with the extremely heavy and the extremely light rockets traveling the shortest distances. This is because the lighter masses will have less propellant and the heavier masses will be too heavy to be lifted and launched efficiently.
We believe that the graph with pressure as the independent variable and distance as the dependent variable will show a positive exponential relationship, because the more pressure applied, the greater the force pushing the rocket forward. Lastly, we predict that the optimum combination will be either 3 or 4 cups at 60psi, for the reasons written above.

Operational Definitions: (Back to top)
Mass- will be defined as the numbers of cups of liquid put into a two liter bottle rocket. Our data set consists of 1 cup to 6 cups.
Pressure- will be determined by the amount read on a pressure gauge. Our data set consists of 30psi to 60psi.
Distance- will be measured in yards by using the football field.
 

Procedures: (Back to top)

Place the launcher at the 0 yard line of a football field facing into the field, prop it up at an angle with something heavy i.e. a bucket etc. take a picture with a camera at ground level to analyze later to find the launch angle. Fill rocket with the set amount of water. Place rocket over PVC pipe and attach metal clip to secure it in place. Now, with someone watching the pressure gage, begin pumping the bicycle pump until the desired pressure is reached. Once this occurs, stand back and pull the rope attached to the metal clip to release the rocket. Now walk onto the field, find the rocket and record the amount of yards it traveled. Repeat this process with three trials for each for data point. (It is recommended to keep one of the variables consistent while manipulating the other, ex- 2 cups at 30psi, 2 cups at 40psi ... then switch to 3 cups at 30 psi, 3 cups at 40 psi... etc.)
 

Data: (Back to top)

Raw Data:

(Trials indicated by commas; numbers in yards)

 

30 psi

40 psi

50 psi

60 psi

1 cup

23, 29, 26

34, 31, 30

33, 31, 34

44, 44, 41

2 cups

34, 27, 29

30, 32, 31

39, 36, 33

36, 41, 45

3 cups

43, 35, 38

36, 40, 35

42, 39, 43

42, 38, 45

4 cups

37, 37, 39

35, 39, 41

39, 43, 42

29, 37, 33

5 cups

30, 27, 28

37, 44, 37

41, 38, 43

30, 31, 34

6 cups

22, 20, 18

26, 26, 20

31, 33, 24

29, 34, 31

Data File (text tab delimited)



Averages (Back to top)
(in yards)

 

30 psi

40 psi

50 psi

60 psi

1 cup

26

31.333333

33

37

2 cups

30

31

36

43

3 cups

39

37

41

42

4 cups

38

38

41

33

5 cups

28

39.666666

41

32

6 cups

20

24

29

31.33333333

Data File (text tab delimited)



Calculated uncertainty values (Back to top)
(in yards)

 

30 psi

40 psi

50 psi

60 psi

1 cup

+/-3

+/-2

+/-1.5

+/-3

2 cups

+/-3.5

+/-1

+/-3

+/-1.5

3 cups

+/-3.5

+/-2.5

+/-2

+/-3.5

4 cups

+/-1

+/-3

+/-2

+/-4

5 cups

+/-1.5

+/-3.5

+/-2.5

+/-2

6 cups

+/-2

+/-3

+/-3.5

+/-2.5

 

     

 

Graphs (Back to top)

 Conclusion: (Back to top)
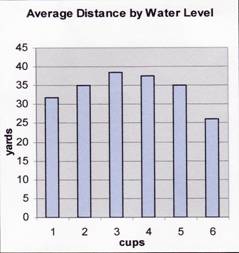
Our first hypothesis (that the relationship between the amount of water and the distance traveled by the rocket would resemble a bell curve) was correct. When all of the trials were averaged together (Average distance by Water Level) a bell-shape curve is clearly visible, and just as we predicted, 3 and 4 yielded the farthest rockets. This was most likely because of the same reasons we mentioned in our hypothesis: the lower masses don't have as much thrust power as the middle ones, but the heavy masses are weighted down by their extra mass more than the additional thrust power compensates for it. 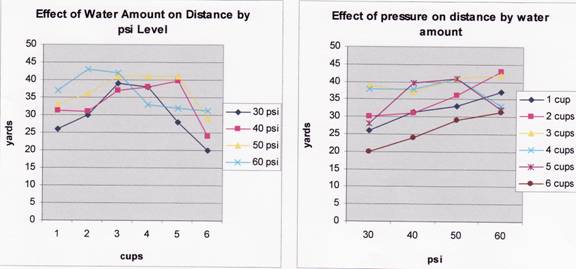In addition to being seen independently, this bell curve is also seen across varying psi levels (Effect of Water Amount on Distance by psi level). The best example of this, is with the "30 psi" values, however, for each level the effect is observed. The fact that this effect is seen in both the independent and collective graphs suggests greater certainty of this outcome.
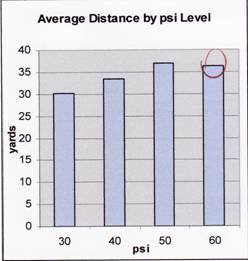
Our second hypothesis, however, was not as clear cut. While the distance increased as the psi level increased when 1, 2, 3 or 6 cups were used (Effect of Pressure on Distance by Water Amount), the data for both 4 and 5 cups heavily drops at 60 psi. These two discrepancies were enough to cause no effect to be observed when psi levels were analyzed independently (Average Distance by psi Level). We attribute this mostly to error rather than any scientific phenomenon. For example, half way through conducting the 5 cup series, we ran out of water, and had to go get more. Because it was cold outside, we decided to put warm water in so our hands wouldn't get as cold, forgetting that a change in temperature would probably have an adverse effect on the graph. In addition, often our rockets didn't fly completely straight, which caused them to land before they had reached their full potential distance. Our calculated uncertainty for each data point was also very high, almost making the discrepancies we did observe between values obsolete. These factors, in addition to others, may have been what caused 60 psi to not show as high of results.
Our third hypothesis would suggest that the farthest distance should have been reached at either 3 or 4 cups, and 60 psi. While the absolute highest value obtained (45) was at 3 cups and 60 psi, the highest average was actually found at 2 cups and 60 psi (43 versus 42 for 3 cups and 60 psi). Although this value doesn't completely match our hypothesis, it does fit in with the general idea that a high psi level and a moderate amount of water is the optimal combination in order to achieve the greatest distance.
Were we to do this experiment again, we would want to use video analysis to allow us to also calculate the vertical displacement. This would allow us to also analyze whether higher pressures cause the rocket to go higher in addition to farther.
 

 

Bibliography: (Back to top)
(1) Slife, Erika. "Imaginations soar in elementary school's water rocket seminar."

    Sun-Sentinel [Fort Lauderdale, FL] 5 Nov. 2006:
 

(2) Singleton IV, Leo C. Bottle Rocket Handbook. 2001. 7 Nov. 2007

    <http://www.pulsejets.com/phpbb2/files/_rocketry bottle_rocket_handbook_952.pdf>.


(3) "How Water Rockets Work." Water Rocket Porta1.26 Jan. 2007. 7 Nov. 2007

    <http://wrockets.trib-design.com/index.php?project=NICK&page=howtheywork>.


(4) Braeunig, Robert A. Rocket Propulsion.] Jan. 2007. NASA. 7 Nov. 2007

    <http://www.bracunig.us/space/propuls.htm>.


(5) Glazier, Colin and Spindel, Aaron. Bottle Rockets. May. 2001

    < http://tuhsphysics.ttsd.k12.or.us/Researcti/lbOI/SpinGlaz/index.htm>

 

Related Links: (Back to top)