Trebuchet Time

Lexxy Johnson, Erica Brabeck, Erin Connelly

Special Thanks to The Sponsels

Introduction:
Background Information: Since the dawn of humankind, people have been fighting one another. With sticks and stones at first, then spears, then slings, then ballistas and catapults until finally, around 400 BC, the trebuchet was born in ancient China. 200 years later, it was introduced to Europe and was used until around the 16th century AD. A Trebuchet is a siege engine used to smash walls by throwing heavy and destructive projectiles long distances. A trebuchet uses a heavy counterweight attached to a lever arm, to which a sling is attached to the long end. With the long arm at ground level, the sling is loaded with a projectile and secured to the ground. When the sling is released, the counterweight falls with great force and propels the sling and the projectile into the air, often to great lengths. Some variables to be considered when building your trebuchet are counterweight, release angle and arm length.
Statement of Problem: The purpose of this investigation is to research the relationship between the weight of projectiles launched by a trebuchet and the distance traveled by said projectiles.
Review of Literature: We decided to focus on journals and articles relating to the mass and acceleration of projectiles and formulas involving the conversation of energy. According to Bob Kibble of Physics Review (2005), a simple model for a trebuchet is possible by considering the conservation of energy formula: MgH = 1/2 mv^2+ mgh. Using this formula, we can predict and calculate the launch velocity if we know the weight and height of the counterweight when cocked and loaded, the weight and range of the projectiles and gravity. According to Porter and Tremblay of The Physics Teacher (2001), the principles of energy conservation can be researched using the trebuchet. Trebuchets use gravity and weights to launch projectiles into the air and at enemies. Paul E. Chevedden details the history of the trebuchet as a siege weapon and it’s architecture, principle of design and the physics of the trebuchet in his article in The Scientific American (1995).
Hypothesis: We believe that the heavier projectiles will travel a farther distance (m) when launched and will also launch at a higher velocity (m/s). Velocity is defined as the speed of the projectile at time of launch. Therefore, if we launch projectiles varying in mass, then the larger projectiles will travel a farther distance and have a higher velocity, because the larger mass creates a greater amount of force and due to the larger mass there is less air friction acting against the projectile.

Method:
The materials we used to complete this experiment were a trebuchet, 9 1 gallon milk jugs filled with varying amounts of water, cones to block off the road from cars, measuring tape and a video camera for documentation. Our setup looked like this:

We chose to launch the trebuchet in a driveway facing out of a cul du sac because the trebuchet is extremely difficult to move great distances. Our procedure was as follows: Load the trebuchet by attaching the projectile to arm (when cocked, no one is allowed to walk in front or behind trebuchet in case of 1,000 pound counterweight falling and killing you), release arm, measure distance traveled by projectile, record, repeat until 9 trials with 3 different masses of projectiles.
We recorded masses of projectiles, height of trebuchet, weight of counterweight, range traveled by projectiles and height of counterweight when cocked. The formula we then used is: MgH = ½ mv^2 + mgh. M is mass of counterweight, g is gravity (9.8 m/s), H is height of the counterweight, m is mass of projectile and h is height of projectile at launch.

Results:

Data Files

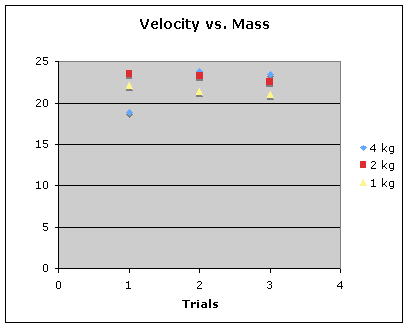
The graph above shows the velocity of each trial. To find the initial velocity we used the
formula √((d/t)^2+ (gt/2)^2). The d is distance (range), t is time, and g is gravity (9.8 m/s).

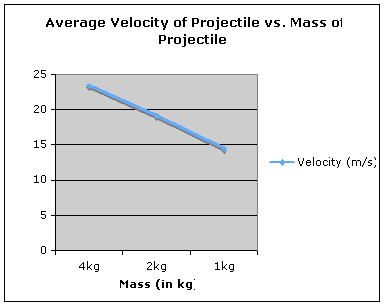
This graph portrays the average velocity of the projectile. As you can see the velocity decreased as the mass of the projectile decreased. This is a direct correlation.
There are many places throughout our procedure that mistakes may have been made. When measuring the range, we may have been off by about one half of a meter. This would be due to human error. Secondly, we measured the time by watching the videos from the launches. We may have been incorrect on the time, due to the lag in reaction time of a human. There is uncertainty in the velocity due to the uncertainties of our variables.
The formula we used for the uncertainty was: x/v=∆t/t+ ∆d/d+ ∆m/m. We calculated the uncertainty for each trial and then averaged the uncertainties. Our average uncertainty for our entire data collection was: +/- 2.94179 m/s. This larger uncertainty, we believe, was due to our larger uncertainty of the time.

Discussion:
Our data supported our hypothesis! Our graph shows a decrease in velocity as the mass of the projectile decreases. Our graph and data were very consistent.
We initially planned on using the conservation of energy formula, but we realized there were too many inconsistencies with the velocities we were calculating. This happened because there were too many factors reducing the energy of the projectile, such as arm swing, way the projectile was released, and the movement of the trebuchet after each launch. Therefore, we decided to use a standard formula for the projectile velocity upon leaving the Trebuchet. Which is √ ((d/t)^2+ (gt/2)^2).
There were places of uncertainty, especially in the measurement of the time. However, our graphs and data support our underlying hypothesis.
If one was interested in doing further research on the trebuchet some other variables that could be tested are the length of the arm, the mass of the counterweight and the effect of adding wheels. The wonders of the trebuchet allow for unlimited experimentation and scientific discovery if one has an open mind and a good sense of adventure. Happy Trebucheting!

Bibliography

“A Harmless Fling” General Reference Center Gold (Feb. 2005):18.

Chevedden, Paul E.. “The Trebuchet” The Scientific American (July 1995).

Hadingham, Evan. “Ready, Aim, Fire.” The Smithsonian (Jan. 2000): 78.

Paul Kibble. “Physics Review.” General Reference Center Gold. (April 2005): 26.

Porter and Tremblay. “The Physics Teacher.” The Professional Collection.

(Nov. 1994): 476.

Related Links:

http://www.trebuchet.com/--All about the trebuchet

http://heim.ifi.uio.no/~oddharry/blide/vtreb.html--A virtual trebuchet! Fling objects of different masses.

http://www.globalspec.com/trebuchet/--A festive game where you get to actually BUILD your own trebuchet...exciting!

http://www.belfry.com/fuzzball/trebuchet/--FAQ about trebuchets.

http://www.redstoneprojects.com/trebuchetstore/trebuchet_history.html--History and Mechanics of the Trebuchet