Efficiency Of Hotwheels® Cars With Rolling Friction
Jeff Jansen & Matt Albertson
IB Physics 2
Background X Statement X Review Of Literature X Hypothesis X Materials X Procedures
Diagram X Data Analysis X Bibliography X Return To Research X Links X Special Message
Very few physicists know about the hidden utilities of Hot-Wheel cars. In fact, most people just assume that they are little toys for their children to demolish. In reality, Hot-Wheel cars can be used to find the percent energy loss as a car object rolls down a slope. The percent energy loss of a hot-wheels car can be calculated by finding the kinetic energy of the car at the bottom of a slope with the formula E=1/2mv^2 (where E is the energy, m is the mass of the car, and v is the velocity of the car) and then dividing this by the cars potential energy which is found with the formula E=mgh (where E is the energy, m is the mass of the car, g is the acceleration of gravity, and h is the starting height). By changing the starting height of the car, the percent energy lost should change as well. The force that allows energy to be lost include air friction, static friction, and most importantly rolling friction.
Statement of the Problem: Go Up
The purpose of our experiment is to find the relationship between the predicted energy of a hot-wheel car and the actual energy of the same car.
We are going to use the potential energy of a hot-wheels car at the top of a ramp, and its kinetic energy at the bottom of the ramp to find the percent energy loss due to friction. This loss of energy would be due to the force of friction on the car from the air and from the track. “A rotating tire’s point of contact is momentarily static, so the tire is slowed by static friction. A skidding tire is slowed by kinetic friction” (Gamick and Huffman). The fact that the tire is momentarily static due to friction will affect the final velocity, even if it is in a very small manner. The main type of friction that we believe will slow the car is rolling friction. “Rolling friction is the friction between a rolling wheel and the plane surface on which it is rolling” (ed. Alan Isaacs). Seeing as the hot-wheel car moves on four wheels, the rolling friction between the track and the wheels will be the main determinant in the loss of energy. “The major source of energy loss during rolling motion is primarily due to the deformation that occurs when the two surface are compressed and relaxed”(webphysics). This reinforces the idea that most the energy lost will in fact be due to the rolling friction, even though some will result from static friction and air friction. The source of this energy is the force of gravity between the earth and the car. The positive accelerations that gravity provides will become the car’s velocity. T. Jackman defines velocity as “the rate of change of its displacement from a fixed point” (Jackman, 1968). The velocity of the car at the bottom of the track is essential to finding the cars final kinetic energy (E=1/2 mv^2; Where E is the energy, m is the mass of the car, and v is the velocity of the car). By dividing the final kinetic energy by the original potential energy (E=mgh; Where E is the energy, m is the mass or the car, g is the acceleration of gravity or 9.8 m/s, and his the starting height above a reference point) we can determine the percent of energy lost to friction.
The starting height of the car is our independent variable as we manipulate it. Our dependent variable is going to be the velocity of the car at the end of the track. We plan to use the mass of the car and the force of gravity to find the potential energy the car has at the top of the ramp, and then use the velocity and mass at the end of the ramp to find the kinetic energy. By dividing the final energy (kinetic) by the potential) we will find the percent energy loss. This energy will be due mainly to friction.
We know that as the starting height of the car increases, so will the potential energy. This means the force of friction between the track and the car will not be as great. We believe that as the ramp height increases, the kinetic energy at the bottom of the track will be more accurate, therefore making the percent energy lost smaller .In an ideal situation, the percent energy lost would be zero.
- Plywood- to make foundation, ramps, and ramp support beams.
- Hotwheels™ Brand Race Cars
- Hotwheels™ Brand Race Track
- Staple Gun
- Angled Table Saw
- Vernier Photogate
- Bolt locks
- 3 by 5 note card
- Meter stick
1. Gathered materials
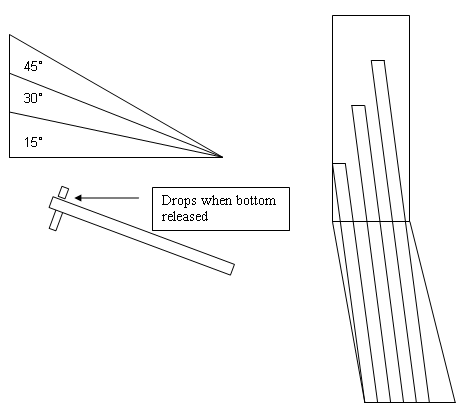
2. Cut plywood into a 90˚ frame for ramps to rest upon
3. Cut three plywood ramp supports; one at 15˚, one at 30˚, and the final at 45˚.
4. Attached Plywood support ramps to plywood frame
5. Attached Hotwheels™ race tracks to plywood support ramps
6. Drilled holes for the bolt locks to act as the starting mechanism
7. Set up Vernier™ Photogates over track
8. Cut and attached 3 by 5 note card to Hotwheels™ Car
9. Used Vernier™ software to find the velocity of the car as it rolled down the tracks
10. Started photogate at the end of the track and record three points of data.
11. Moved photogate back 2 decameters and repeated step 10.
12. Stopped recording data once photogate was one meter away from the end of the plywood frame.
13. Masses Hotwheels ™ Car.
14. Measured the height of the release points on the tracks.
15. Used E=mgh and E=1/2mv^2 to find the amount of energy lost due to friction.

Data Analysis: Go Up : Data File
We decided that to eliminate a higher uncertainty, we would do each trial three times. We recorded the velocities of the car as it raced down the tracks at the different degree measurements. Our data included the following:
|
Velocity (m/s) |
|||
|
|
15 |
30 |
45 |
|
0dm |
2.575;2.582;2.579 |
Track Not To End |
Track Not To End |
|
2dm |
2.592;2.567;2.567 |
3.655;3.488;3.532 |
Track Not To End |
|
4dm |
2.395;2.444;2.413 |
3.741;3.622;3.67 |
Track Not To End |
|
6dm |
Experimental Design Error |
3.402;3.362;3.362 |
4.287;4.302;4.303 |
|
8dm |
2.069;2.70;2.069 |
3.107;3.132;3.127 |
4.185;4.118;4.162 |
|
1m |
1.878;1.880;1.892 |
2.874;2.801;2.810 |
3.720;3.728;3.695 |
15˚ Work:
Average Velocity:
0dm: (2.575+2.582+2.579)/3= 2.579 m/s
2dm: (2.592+2.567+2.567)/3= 2.578 m/s
4dm: (2.395+2.444+2.413)/3= 2.417 m/s
6dm: Experimental Design Error
8dm: (2.069+2.070+2.069)/3= 2.069 m/s
1m: (1.878+1.880+1.892)/3= 1.883 m/s
Uncertainty: (high-low)/2
0dm: (2.582-2.575)/2= .0035 m/s
2dm: (2.592-2.567)/2= .0125 m/s
4dm: (2.444-2.395)/2= .0245 m/s
6dm: Experimental Design Error
8dm: (2.070-2.069)/2= .0005 m/s
1m: (1.892-1.878)/2= .007 m/s
30˚ Work:
Average Velocity:
0dm: (2.575+2.582+2.579)/3= 2.579 m/s
2dm: (2.592+2.567+2.567)/3= 2.578 m/s
4dm: (2.395+2.444+2.413)/3= 2.417 m/s
6dm: Experimental Design Error
8dm: (2.069+2.070+2.069)/3= 2.069 m/s
1m: (1.878+1.880+1.892)/3= 1.883 m/s
Uncertainty: (high-low)/2
0dm: (2.582-2.575)/2= .0035 m/s
2dm: (2.592-2.567)/2= .0125 m/s
4dm: (2.444-2.395)/2= .0245 m/s
6dm: Experimental Design Error
8dm: (2.070-2.069)/2= .0005 m/s
1m: (1.892-1.878)/2= .007 m/s
G. W. Hammar; Gordon Martin. “On the Nature of Friction”. Science, New Series, Vol. 90, No. 2330. (Aug. 25, 1939), pp. 179-180. Stable URL: http://links.jstor.org/
Gamick, Gary and Art Huffman, The Cartoon Guide to Physics. Harper Collins Publisher, New York. 1990.
A Dictionary of Physics. Ed. Alan Isaacs. Oxford University Press, New York. 1996.
T. Jackman. The Mathematical Gazette, Vol. 52, No. 379. (Feb., 1968), pp. 48-49. Stable URL: http://links.jstor.org/
Michael Lassiter. “Rolling Friction” <http://webphysics.davidson.edu/faculty/dmb/PY430/Friction/rolling.html>
http://www.glenbrook.k12.il.us/gbssci/phys/mmedia/energy/hw.html : This webpage provides information on the stopping distance of a Hot Wheels car due to rolling friction as it comes down an incline.
http://www.powermasters.com/Mini%20Lessons/Friction/friction.html : This webpage gives a basic overview of the effect of rolling friction and how to calculate it.
http://www.sciencebyjones.com/hot_wheels_energy.htm : This webpage gives possible labs that students can do quite easily which involve friction and Hotwheels and/or Matchbox cars.
http://www.britannica.com/eb/topic-507149/rolling-friction : This is Encyclopedia Britannica's definition of rolling friction. This was our working definition.
http://www.newton.dep.anl.gov/askasci/phy00/phy00698.htm : This is basically a forum that identifies rolling friction and answers some basic questions about it.
http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html : An overview of the main four types of friction with examples and images.
http://www.google.com/ : Our search engine :)
GO OREGON STATE BEAVERS!!!!!!!!!!!!!!!!!!!!!
And McDaniel Green Terrors