The Optimum Arm Ratio of a Trebuchet

Kyle Carpenter

David Torbeck

Table of Contents .:. Return to research

• Background

• Question

• Literary Connection

• Hypothesis

• Materials

• Procedure

• Data Collection

• Data Analysis

• Conclusion

• Pictures

• Bibliography

Background

            First used in Ancient China with men pulling as a counterweight in a crude design, trebuchets traveled across the silk road to the Middle East and eventually Europe to be used as a very effective siege engine.  There they reigned for 200 years as the main way to break down a castle wall until the advent of gunpowder weapons.  A siege engineer that could build a trebuchet was of great value to any king as it took precise calculations and handiwork to build not only a functioning trebuchet but one that could knock a hole into a wall from a certain distance.

             Composed mainly of wood with metal supports and either a counterweight made of dead weight (usually lead) or a box for which the weight could be altered, the idea behind the trebuchet was that the counterweight could bring the projectile full circle for a greater arc and therefore a greater throwing distance and force.     Also, adding wheels could further stabilize the siege machine and enhance the throwing distance of the projectile. 

            Trebuchets were a mainstay of the medieval army and continue on as a symbol of medieval siege warfare.

Question

            How does the arm ratio on a trebuchet affect it’s horizontal velocity?

Literary Connection

            There are lots of different variables that we could change on our trebuchet, but we chose the ratio between the counterweight arm and the throwing arm.  So we will be measuring the horizontal velocity of the projectile as a result of the arm ratio.  The optimum arm ratio has factors like beam mass and counterweight mass, as well as beam shape (M Denny).  The trick to finding an optimum arm ratio is to balance the leverage with the speed of the throwing arm (ripcord.ws).  Dan Becker suggests that the optimum arm ratio is 4to 1 or greater.  Philip Radlinski explains that as the size of the throwing arm increases, the distance the projectile is thrown increases then rapidly decreases.  This means that the shape of the graphed results will most likely be an inverse parabola.

Hypothesis

            If the distance thrown is dependent on both the leverage of the counterweight arm and the speed of the throwing arm, then our data will resemble an inverted parabola with a peak at the ratio of 5:1 because as the counterweight arm gets shorter, the force will decrease due to being so close to the fulcrum, and as the throwing arm gets shorter, the force will increase due to being so far from the fulcrum.

Materials

·        Trebuchet with variable arm ratios

·        Meter tape

·        Stop watch

·        1 pound solid projectile

Procedures for testing the trebuchet

1.      Set up the trebuchet

2.      Set out a meter tape starting from the front of the base and lay on ground

3.      Move the arm to position 1

4.      Load the trebuchet

5.      Launch the trebuchet

6.      While the trebuchet is bieng launched, time the throw from when the projectile leaves the sling to when it hits the ground

7.      Record the distance and time on a piece of paper

8.      Repeat steps 4 – 7 to get two more trials on this arm ratio setting

9.      Repeat steps 4 – 8 for all ten settings

10.  Clean it all up

Data Collection

  Data File (Text) (Excel)

Data Analysis

Conclusion

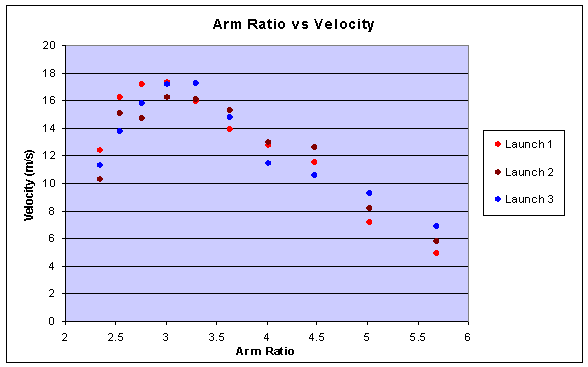
            Our hypothesis was not supported because the optimum arm ratio seemed to be 3:1 and not 5:1.  This happened because at 5:1, there was not enough power to lift the arm and the projectile and still have enough energy to throw the projectile at a high velocity.  On the other hand, at the 3:1 ratio there was just the right balance between leverage and speed of the arm to achieve the highest velocity.  Some errors that we might have had in our experiment include, wind, measuring, and the axel connection.  The wind could have caused us errors by blowing our projectile off to one side, pushing it forward, or pushing it backwards.  Some errors that we had in measuring could have happened because we laid the meter tape on the ground in a stationary position and no matter how far to the side of the tape the projectile landed, we just looked at the meter tape and guessed the distance.  Another error in measurements that we had was in the timing.  The person who was timing started the watch when the projectile was released and stopped it when it landed, which could have been 60 M away.  With starting and stopping points this uncertain, there could have been many timing errors.  Another error that could have occurred was the axle connection.  Because we drilled the holes for our first axle and had to change the axle when the first one that we made broke, the connection between the new axle and the arm was loose and sometimes sliding around.  To fix these errors, we could test it on a less windy day, be more careful timing, and drill the holes for the smaller axle in the first place.

Pictures   

Bibliography

            http://www.io.com/~beckerdo/other/trebuchet.html  -  Plans and directions for building a small trebuchet

http://www.tbullock.com/trebuchet.html  -  History behind the trebuchet 

            http://www.ripcord.ws/theory.html  -  Theory and mathematics of trebuchets

            http://www.algobeautytreb.com/ -  Algorithms of a trebuchet

            http://www.legionxxiv.org/trebuchetpage/  -  History and details of the trebuchet

  Return to top