Introduction TOP
Problem:
We will be testing the relationship between the pullback length of a tubular catapult and the initial velocity of the projectile. Our different pullback lengths will be 5, 10, and 15 inches (which we will later convert into metric units).
Background:
The method of tubular catapults can be used for simple things such as spit wad shooters and pinball machines. A projectile is launched after pulling the inside rod back and quickly released. Our experiment is fundamentally a test of how the velocity changes based on the length pulled back. We know that a 45-degree angle will produce the same initial velocities for horizontal and vertical.
Hypothesis:
We believe that the relationship between the pullback length and the initial velocity will be linear.
Method TOP
Procedures:
1. Obtain the necessary materials (PVC pipe, surgical tubing, hinges, clamps, wooden rod, wood for mounting, projectile, etc.)
2. Build catapult
3. Set up catapult
4. Launch ball at a pull back-length of 5 inches
5. Measure and record
6. Repeat steps 4-5 10 times
7. Repeat steps 4-6 using lengths of 10 and 15 inches
8. Clean up and complete calculations
Experimental Set-up:
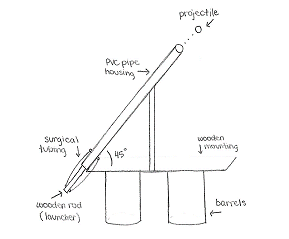
Our set-up was not complicated. We mounted the catapult on two barrels so that we would be far enough off the ground to allow for long enough pullback lengths. The wooden rod was marked every inch for measuring. We secured the angle at 45 degrees by using a protractor. Then we laid out two measuring tapes beginning at the end of the tube and covering fifty feet. Finally, we placed the ball in the end of the catapult and launched it, ten times for three different lengths. The set-up was very successful though not exactly ideal.
We used PVC piping and a wooden rod because they seemed like the most stable materials for the actual catapult. Surgical tubing was used for the elastic connecting the wooden rod to the pipe because it returns to its original shape after being stretched. The catapult is on hinges, which gives us options for further experimentation with the effects of changing the launch angle. The chosen projectile was a bouncy ball. This choice was most convenient initially, but after losing two (down sewage drains and in the neighbor’s yard) we would have liked to choose something less bouncy.

Results TOP
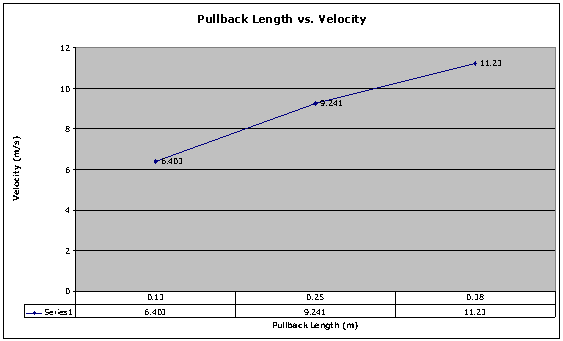
Our hypothesis was not exactly right and not exactly wrong (to put it scientifically). The data shows a relationship similar to a line, but not exactly. This could be because of errors during the experiment. Or it is possible that the relationship is not linear at all. We realize now that in order to get a solid conclusion we should have tried more pullback lengths. It is hard to tell what the actual relationship it, although it is obvious that the velocity increases as the pullback length increases.
Discussion TOP
Errors:
In this experiment there were plenty of errors, or uncertainties to consider. First, there was human error in the reading of range, pullback length, and angles. We considered all of these errors when evaluating our results. There was also wind during our experiment that could have contributed to the lack of accuracy.
Further Exploration:
It is very easy to find the problems in our experiment, namely the bounciness of the ball, the quality of the weather, etc. Obviously we with more time we could pick an ideal day and perhaps record the experiment on video to get more accurate measurements. Further exploration would definitely include making necessary improvements. The first thing would be to imitate our initial experiment and test more pullback lengths to clarify what the relationship between velocity and pullback length actually is. We also want to see what changing the angle will do to the projectile (which most likely won’t be a bouncy call again). We could test different masses of balls and consider that effect.
Bibliography
Giancoli, Douglas C. Physics, Principles With Applications. New Jersey:
Prentince Hall. 1980.
Pearsall, Judy. Oxford English Dictionary. Oxford University Press, 1996.
Kittel, Charles. Mechanics; Berkeley Physics Course Vol. I. 1965. 248
Additional Links
The trebuchet projectile follows the same pattern and launch characteristics as the tubular catapult. This website goes over the algorithmic beauty of the trebuchet. It also has a simulation and discusses effective materials while making a perfect trebuchet.
www.ocps.k12.fl.us/framework/link.php?benchmark=591
This website provides additional web pages to click on in order to understand fundamental principles that deal with our experiment, including gravity, force, motion, and Newton's laws.
www.lcse.umn.edu/specs/labs/catapult
Projectile motion equations and mathematical difficulties involved in our experiment are gone over in this website. It was very helpful in determining which equations to use and modify.
http://hyperphysics.phy-astr.gsu.edu/hbase/traj.html
This link is about hyper physics. It goes over freefall, trajectory, horizontal launch and several other principles that apply to tubular catapults and the motion of the projectile after it leaves the tube.
http://www.howstuffworks.com/physics-of-football2.htm
Footballs have similar flight patterns to our projectile and this web site explains how to calculate range and hang time for a football.