Introduction Background Information

FREE THROW PHYSICS

By: Kate De Paepe

Table of Contents

Introduction

Return to Research Page

Introduction Up
Background Information-
    The game of “basket ball” was invented by Dr. James Naismith in 1891 on orders to provide students with a sport that could be played indoors during the winter months. Starting with only “18 men in a YMCA gymnasium in Springfield, Massachusetts,” basketball has grown into one of the most recognized sports worldwide [2].Even with the original and limited 13 rules, the purpose of the game was to outscore the opposing team, with points being awarded each time a player successfully placed the ball into the basket. Today, though that purpose remains unchanged, the sport has evolved into a game of skill and strategy. For instance, although Naismith originally intended for each basket to be worth one point, there are now three increments of point values in basketball: the two-pointer, the three-pointer, and the free throw (one point). However, some might say that the value of points is directly related to the difficulty of the shot- enter strategy. Specifically, the point value increments go as follows: three points are awarded for any made-basket behind the three-point line; two points are awarded for any basket made within these dimensions; free throws are awarded when a shooting or bonus foul is called on the opposing team (the free throw line is “15 feet from the backboard” [1]). Thus, the three-point shot is arguable the most difficult because it requires the most strength and accuracy. The two-point shot can be as easy as one foot from the basket to as difficult as just inches inside the three-point arc. Free throws, although they are a significant distance from the basket, are dubbed by many as the easiest shot in basketball because they are shot facing the basket dead on, and are awarded without defensive pressure. By looking at basketball statistics, one can see that the percentage of making a shot goes from highest at the free throw line to lowest from behind the three point arc. This is because the percentage of making a shot (or the accuracy) is dependent on many factors of physics such as velocity, kinematics, projectile motion, gravity, etc. The further a person is from the basket when they release the ball, the more time these factors are allowed to impact the accuracy of the shot.

Statement of the Problem-
    The purpose of this experiment is to find the relationship, if any, between the angle the ball approaches the rim (independent variable) and the accuracy of the shot (dependent variable), when shot from the free throw line.

Review of Literature-
    In the game of basketball, there are so many different variables involved in shooting that it is impossible for any two or more shots to be exactly the same. Some such variables include the angle at which the ball is released as well as the angle it enters the basket, it’s vertical displacement (arc), the height of release, the initial velocity of the ball leaving the shooter’s hand (how much force is put into the shot), the ball’s motion through the air, and the straightness of the shot [5]. As is pointed out in the physics textbook [2], the effects of air resistance can often be ignored in analysis. One study, regarding the physics of shooting in wheelchair basketball, focused specifically on that involved in free throw shooting. More or less, their findings were based on the height of release, the angle at which the ball left the shooter’s hand, and the amount of force put behind the shot. The findings showed that “the higher the point of release, the more likely the shot will be successfully,” while higher angles of release (perhaps from releasing the ball at a lower point) demand greater accuracy, which attributes to the lower percentage in free throw shooting found in wheelchair basketball [4]. Though obviously wheelchair basketball players are at a major disadvantage (without the ability to use lower body strength and regarding their increased distance from the basket) compared to standing basketball players, the results of this study nonetheless have significant implications. Most importantly, the many seemingly insignificant variables of shooting do indeed have notable impacts on the accuracy of the shot. I will try to minimize the inconsistency in these variables over the course of my experiment. Nonetheless, as Fred Newman (“Guinness Book of World Records” holder for most free throws made in one hour- 2,034- in 1996) points out, the main idea in successful shooting is to shoot “the ball high enough to maximize the target's size, and low enough that it doesn't travel any farther than it needs to" [7]. This supports the idea that the angle at which the ball approaches the rim plays a key role in the probability of the shot going in and that the most accurate shot would be one that descends into the basket at a perpendicular angle, as this would maximize the area of the rim.

Hypothesis-
    I believe that graphically (with the angle of the shot as the independent variable and accuracy as the dependent variable) my results will resemble a semicircle, with the extremely low and extremely high angled shots being the least accurate. This is because shots that enter the plane of the rim at a greater height will require an increased angle of trajectory (which has direct effects on accuracy [4]), and will most likely go too far. Conversely, those that approach the basket at lower angles minimize the area of the rim, and consequently, the probability of going in. I will strive to find an angle at which the shot is most accurate. Angles will be measured in degrees. Accuracy is defined in relation to the cleanliness of the shot (with a clean shot being defined as “a successful shot that passe[s] through the hoop without hitting the rim or backboard” [4]), in which a scalar evaluation will be used.

Method Up
    In order to understand and replicate this experiment, it is first necessary to understand how the results are obtained. This includes the experimental setup (method used to collect raw data), data collection (how to record and organize raw data), and the application of relevant formulas in order to interpret the results. The following description of these methods will provide insight to do so.

Experimental Setup-
    The objects needed to complete this setup and perform the experiment include: a standard basketball hoop and court, a customized poster-board*, a digital camcorder with tripod, and a standard women’s basketball. The camcorder should be place perpendicular to the basket (so that the shots can be filmed from a side view), and at a height where it can capture the ball slightly before it passes over the rim. It is not necessary to see the shooter or the majority of the course of the ball’s path towards the basket. The experimental setup is diagramed on the following page.

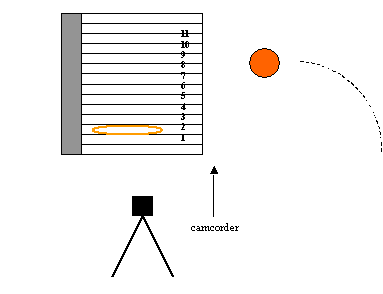
Figure 1

*This experiment requires the use of a device that measures the height of the ball just before it passes over the rim. The simplest way to do this is to create a poster board with evenly spaced lines precisely one centimeter apart. The lines should be labeled with their respective measurements (1, 2, 3, etc.). This poster can then be attached to the backboard so that it runs parallel to the rim, as is diagramed in Figure 1 above. The poster-board should measure at least 42 inches (the height of the backboard) by 30 inches (the length of the backboard to the rim, plus six inches extra for measuring purposes).

Data Collection-
The main purpose for the use of the camcorder is applied in the data collection process of the experiment. In order to collect data for this experiment, it is only necessary to focus the camera around the rim. A suggested view is diagramed below:

Figure 2

This view provides for the height of the ball to be analyzed after all the data is collected. The height of the ball should be measured before it crosses the rim, and from the bottommost point of the ball. This is detailed in Figure 3 below. Further, since the camera will be so focused on the front of the rim and zoomed in to see the measurements on the poster-board, it will not record the actual shot. Thus, one person should be designated to record the details of each shot. It is suggested that this person says aloud whether the shot is a make or a miss, and how many times the ball touches the rim or backboard in the process, as the camcorder can record the audio. For example, the recorder might say “make, three bounces,” for a shot that goes through the basket after hitting the rim or backboard three times. All data should be recorded in a table. For the purposes of this experiment, I shot 200 shots. However, the more shots, the more reliable the data.

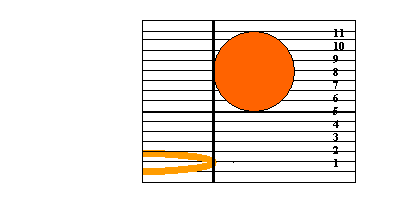
Figure 3
For the purposes of this experiment, the misses will be omitted from the data when it is analyzed and graphed, as the focus of intent concerns only those shots that are successful. However, since the camcorder will not necessarily capture the result of the shot, it is useful to keep track of the data for analyzing purposes.

Formulas and Applications-
    The primary formula applicable to this experiment is the inverse-tangent function. This formula can be applied simply by making a right triangle between the ball and the rim (see Figure 4) using the measurements obtained during data collection, and those measurements already known. The necessary measurements include the length from the center of the rim to the center of the ball (known value) and the height of the ball just before it passes above the rim (raw data).

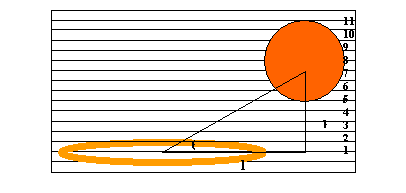
Figure 4
The formula and values are designated as follows:

                                    Tan-1=h/l
where,
    h=the height of the ball above the rim
    l=the length from the midpoint of the rim to the midpoint of the ball, which can be derived by adding           the radius of the rim (9 inches) to the radius of the ball (approximately 4.5 inches). Thus, l serves           as a constant of 13.5 inches.

The simplified formula for this experiment is:

                                   Tan-1=h/13.5

Results Up
    Though with some variation, the results show that the best angle for the ball to approach the rim when shot from the free throw line is between 65 degrees and 67 degrees. The graph illustrates this fact in Figure 5. As is evident, the angles between these two measurements of degree generally generate the most accurate shots (the least number of bounces on the rim). Most notably, angle measures of 65.037 degrees and 67.126 degrees yield only perfect shots. Nonetheless, these results are not without uncertainty. During the actual experiment, it was difficult to control all the mechanics that go into a shot- force, velocity, maximum height, etc. In application, some shots may have approached the basket at the calculated perfect angle, yet were off-center, thus accounting for a missed shot or a “less-accurate” (not totally clean) shot. Such variations are noted, but are also taken in stride, as in reality each shot taken over the course of a game or practice is unique as well. Therefore, the results are still applicable and valid. However, uncertainty in the data analysis can account for a possibility of skewed results. Since the recording was more blurry when transmitted onto a television, sometimes lines and numbers on the poster-board were hard to see. This provides for an uncertainty of one centimeter in those measurements, which could in turn affect the calculated angles. Thus, there is an overall uncertainty of about five degrees, give or take.

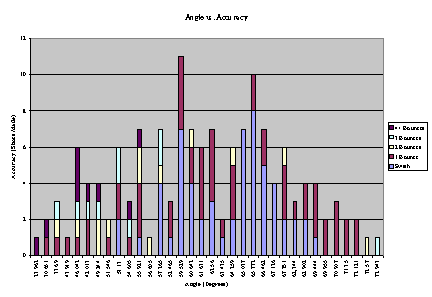
Figure 5

Data File

Discussion Up
    Overall, my hypothesis was supported- the graph of my results resembles a semicircular curve. However, if you look at the angles individually (separate from the general shape of the graph), it seems to undermine the correlation. For example, even in the range of 60 degree angles- in which one might presume would provide for the most accurate shots- there are instances (particularly at 63.435 degrees) where the shots were seemingly very inaccurate. Occurrences like these, nonetheless, can be easily accounted for. For instance, even when a shot may approach the rim at a perfect angle, if the shot is off center it may bounce around before going through the rim, or not go in at all. During the experiment, I considered the value of placing a camera above the rim, and analyzing only those shots that are perfectly clean in order to find a very specific approach angle.
    In fact, suggestions for subsequent research to this experiment are many-fold. For one, I would like to re-do this same experiment, but shoot at least double the shots. It would be interesting to see if the results become more consistent, or more variant. I give the possibility for them becoming more variant because it seems that the many factors that go into shooting a basketball can sometimes compensate for each other. That is, a shot with an angle of approach that may appear too low can be corrected if it is released with greater force and at a faster velocity. Further, it might be of interest to not only study those shots that are successful, but also the shots that miss, in order to find a possible correlation. Also, varying the length from which the ball is shot would give insight to a relationship between distance, height, and accuracy.

Bibliography Up
1. “Basketball Court Dimensions.” Better Basketball, Inc. 2005.
        <http://www.betterbasketball.com/basketball-court-dimensions/>
2. Giancoli, Douglas. Physics: Principles with Applications Fifth Ed. New Jersey:
        Prentice Hall, 1998.
3. “History.” Naismith Memorial Basketball Hall of Fame, Inc. 2004.
        <http://www.hoophall.com/history/history.htm>
4. Malone, Laurie, and Pierre Gervais, and Robert Steadward. “Shooting mechanics
        related to player classification and free throw success in wheelchair basketball.”
        Journal of Rehabilitation Research and Development.
        November/December 2000: Vol. 39, No. 6, p701-710.
5. Rojas, F.J., and M. Cepero, and A. Ona, and M. Gutierrez. “Kinematic adjustments in
        the basketball jump shot against an opponent.” Ergonomics. October 2000:
        Vol. 43, Issue 10, p1651-1660.
6. Wood, Daniel B. “He may not be an NBA star, but this guy sure knows his free
        throws.” Christian Science Monitor. 7 June 1996: Vol. 88, Issue 135

Related Links Up

http://mrfizzix.com/basketball/- This website presents an overview of the various aspects of physics involved in basketball, from passing, to dribbling, to shooting.

http://clackhi.nclack.k12.or.us/physics/projects/NewtonsLaws_2005/d2_4-Physics/rk/our%20webpage.html- This website takes a look at the physics of shooting, with a focus on the contributions of Newton's Laws to understanding the motion of a shot.

http://physics.about.com/od/?once=true&- This website contributes many various links that take an even more broad look at physics as it relates to many aspects of life, including the basics to "real world" physics.

http://www.fearofphysics.com/Proj/proj.html- This website makes the claim that by incorporating the right laws of physics you could make a shot every time. Try it out for yourself!

http://home.nc.rr.com/enloephysics/sports.htm- This website takes a look at the physics in a variety of sports, including basketball. It also offers additional links about the science of basketball.